Ant Colony Optimization, ACO 蚁群算法简单介绍

Created 2021.02.09 by Cong Yu; Last modified: 2021.02.09-V1.0.3

Copyleft! 2021 Cong Yu. Some rights reserved.

ACO

References

0. Basic Concepts

信息素（pheromone）
蚂蚁行进释放信息素，信息素会以一定的速度散发掉
蚂蚁之间可以靠信息素交流
信息素有浓度
图结构中，信息素即图的边的权重
每只蚂蚁都有自己的内存
内存里面存放两张表：
- Tabu（禁忌表）存储已经访问过的目的地表
- Allowed 存储还可以访问的目的地表

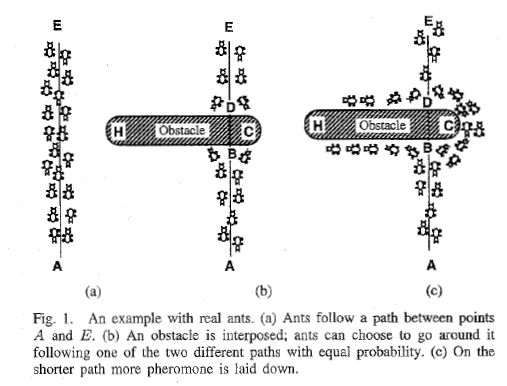
主要可解决的问题 : TSP问题

TSP问题（Travel Salesperson Problem，即旅行商问题或者称为中国邮递员问题），是一种NP-hard问题，此类问题用一般的算法是很难得到最优解的，所以一般需要借助一些启发式算法求解，例如遗传算法（GA），蚁群算法（ACO），微粒群算法（PSO）等等。

1. 算法模型

1.1 数据

m 蚂蚁数量
- Tabu-Allowed 表
- route 蚂蚁走过的路线
c 城市数量
distance 距离矩阵 (c*c矩阵)，各个城市之间的距离信息
pheromone 信息素矩阵 (c*c矩阵) 表示节点与节点之间的信息素量，即图结构中边的权重
- delta_pher 信息素变化矩阵 (c*c矩阵) 存储一个循环（或者迭代）中所有蚂蚁在每条路径上所释放的信息素矩阵，以及信息素衰减矩阵
kMaxGen 最大迭代次数
- iter 当前迭代次数
- tour_length 某蚂蚁走完全程的总成本
- best_path 最佳路径 (1*c 矩阵)
- best_len 最佳路径的长度
logger 迭代日志 (kMaxGen*2 矩阵) [iter, best_len]
控制参数 (α，β，ρ，Q)
- α 信息素因子
- β 启发函数因子
- ρ 挥发因子
- Q 常系数

1.2 解读

m 蚂蚁数量
- m 过大会导致搜索过的路径上的信息素变化趋于平均
- m 过小会使为被搜索的路径信息素减小到0，出现早熟，陷入局部最优解
- 通常设置 m = 1.5 c
Alpha 信息素因子
- 反映历史积累信息量对蚁群探索的影响
- 越大，蚂蚁偏好于选择以前走过的路径
- 越小，等同于贪婪算法，易导致局部最优
- [1,4]区间时，性能较好
Beta 启发因子
- 反映先验性和确定性因素的作用强度
- 越大，收敛越快，易导致局部最优
- 越小，易陷入随即搜索，不收敛
- [3,4,5]区间，性能较好
Rho 挥发因子
- 影响全局搜索能力和收敛速度
- [0.2,0.5]区间内，性能较好
Q 信息素常数
- 表示蚂蚁循环一周释放在路径上的信息素总量
- 越大，蚂蚁在已遍历路径上的信息素积累越快，收敛越快
- 大小取决于路径长度的量级

1.3 算法流程

Init
- 初始化 distance
- 初始化 pheromone，初始数值均为1
随机产生m只蚂蚁分布到c个城市
蚂蚁移动
- 更新每只蚂蚁的 Tabu-Allowed 表
  - 将当前城市从Allowed改为Tabular
- 按照访问规则为每只蚂蚁挑选下一个目标
检查蚂蚁是否已经到过所有城市
- 是，本次迭代结束，收尾工作
- 否，重复步骤3
- 其实就是步骤3重复c次，这样每只蚂蚁就都到过c个城市
更新信息素矩阵
- 计算本轮迭代中，所有蚂蚁走完全程的消耗，找出其中的最小值作为最优解，输出当前最优解
- 按照更新规则更新信息素权重矩阵
  - 需要计算更新矩阵，包含两部分，本轮迭代蚂蚁释放信息素矩阵与挥发矩阵
检查终止条件
- 如果达到最大迭代次数，算法终止，输出最优解
- 否则，重复步骤2,3,4,5

2. 访问规则

为了更好的利用TSP问题自身的性质，M.Dorigo等引入了一个启发项： $\eta_{ij} = \frac {1} {d_{ij}}$
启发项为距离的倒数
蚂蚁选择路径i到j的概率为：

\[p_{ij}^k(t)= \left\{\begin{matrix} {\frac { [\tau_{ij}(t)^\alpha] [\eta_{ij}^\beta] } { \sum_{k\in{allowed-city}} [\tau_{ik}(t)^\alpha] [\eta_{ik}^\beta] } }, j \in allowed_k \\ 0,else \end{matrix}\right.\]

其中

$\alpha$和$\beta$是调节因子，用于调节 $\tau_{\ddot{y}}(t)$ 和 $\eta_{i j}$ 之间的作用
$allowed_{k}$ 表示蚂蚁k还没有走过的路径
如果路径i到j上的信息浓度越大 $\tau_{\mathrm{ij}}(t)$ 的值就越大，该路径被选择的概率就越大
同样，如果该路径长度越短，则$\eta_{ij}=\frac{1}{d_{ij}}$越大，该路径被选择的概率也越大

3. 更新规则

蚂蚁系统采用 $\tau_{\mathfrak{ij}}(t)$ 来模仿t时刻路径i到j上面的信息残留量，即信息素浓度。
如果没有经过ij，则蚂蚁在该路径上的信息素量为0
类似于蚂蚁觅食过程，每条路径上面的信息素会挥发，如果有蚂蚁经过的时候，信息素的浓度会相应增加。
信息素浓度的更新公式为：$\eta_{ij}(t+n) = (1-\rho) \cdot \tau_{ij}(k) + \Delta\tau_{ij}$
- 式中，$\rho \in [0,1]$，为挥发因子。
- 式中， $\Delta\tau_{ij}$ 表示一次旅行（遍历完所有城市）后，所有蚂蚁中路径 i 到 j 上各蚂蚁留下的信息素总量，即：
- \[\Delta \tau_{ij} = \sum_{k=1}^{Ants}\Delta\tau_{ij}^k\]
- 也就是要将本轮迭代中ij路径上经过的所有蚂蚁释放的信息素全加起来
- 式中， $\Delta \tau_{i j}^{k}$ 表示第 k 只蚂蚁在路径 i 到 j 上面留下的信息素量
而对于某一只蚂蚁k，在ij路径上会释放多少信息素呢？三种模型
- 蚁周模型
- 蚁量模型
- 蚁密模型

蚁周模型

释放总量一定，利用路径整体信息计算
考虑全局信息
$L_k$ 为k蚂蚁经过的路径总长
可见，该蚂蚁走的越多，对结果的影响力越小

蚁量模型

释放总量一定，利用局部路径信息
只考虑当前路径信息，当前路径越短，信息越多

蚁密模型

每段的信息释放量确定

Code

// todo(congyu)

Contact

Feel free to contact me windmillyucong@163.com anytime for anything.

License

Creative Commons BY-SA 4.0

Ant Colony Optimization(ACO) 蚁群算法

蚁群算法简单介绍

ACO