AVL

• 二叉平衡树
  • Basic Concepts
    • 二叉树
    • 有序二叉树
    • 平衡二叉树
    • 平衡因子 BF
  • 节点结构
  • AVL自平衡
    • 最小失衡子树
    • 左旋
    • 右旋
  • 插入节点
    • LL: A的左孩子的左孩子上插入节点
    • RR: A的右孩子的右孩子上插入节点
    • LR: A的左孩子的右孩子上插入节点
    • RL: A的右孩子的左孩子上插入节点
    • 总结：AVL的自平衡步骤
  • 删除节点
    • 四种情况
    • 删除操作的大致步骤
  • Contact
  • License

二叉平衡树

Created 2021.04.08 by William Yu; Last modified: 2021.04.09-V1.1.2

Contact: windmillyucong@163.com

Copyleft! 2021 William Yu. Some rights reserved.

References

• https://zhuanlan.zhihu.com/p/56066942

Basic Concepts

二叉树

有序二叉树

• 有序二叉树的缺点：
  • 当原序列本身就有序时，搜索效率降低为O(n)

平衡二叉树

• 平衡二叉树：
  • 搜索效率取决于树的高度，保证树的高度最小
  • 节点数量：n，高度：h
    • $n=2^h-1, h=log_2(n+1)$

  • 时间复杂度 $O(log_2N)$

  • 定义：任何节点的左右子树的高度相差不超过1的有序二叉树
• 性质：
  • 可以是空树
  • 任何节点的左子树和右子树高度差不超过1
  • 任何一个节点的左子树和右子树都是平衡二叉树

平衡因子 BF

• Balance Factor BF
• 定义：某节点的左子树与右子树的高度差
• 平衡二叉树中节点的平衡因子只能取0，1，-1
• BF = 左 - 右

节点结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
template <class T>
struct AvlNode {
  T data;
  AvlNode parent;
  AvlNode *l_child, *r_child;
  int depth;

  AvlNode() {
    parent = nullptr;
    l_child = r_child = nullptr;
    this->data = 0;
    depth = 0;
  }

  AvlNode(T data = 0) {
    parent = nullptr;
    l_child = r_child = nullptr;
    this->data = data;
    depth = 0;
  }
};

AVL自平衡

最小失衡子树

• 插入一个node，之后重新计算每个node的平衡因子，可能有多个node的平衡因子绝对值超过1，这些node失衡
• 最小失衡子树：在新插入的节点向上查找回溯，找到第一个失衡的节点，以该节点作为根的子树称为最小不平衡子树
• 一棵AVL失衡的时候，可能会有多个子树同时失衡，只需要调整最小的不平衡子树，就可能将整个不平衡的树调整为平衡的树
• 平衡方法：旋转最小失衡子树
  • 左旋和右旋

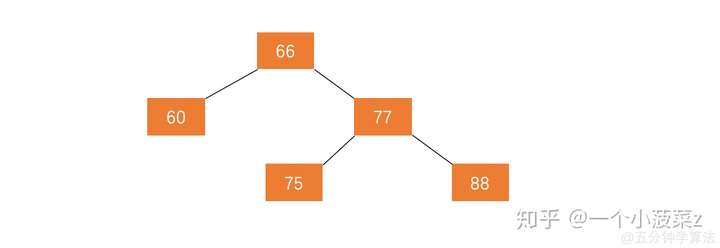
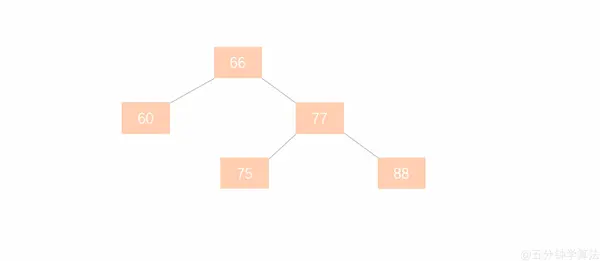
左旋

• BF = 左 - 右

  • 左高右低，BF > 0 ，右旋调整
  • 左低右高，BF < 0 ，左旋调整

• 左旋步骤：

  1. 节点的右孩子替代此节点位置

  2. 右孩子的左子树变成该节点的右子树

  3. 节点本身变成右孩子的左子树

     

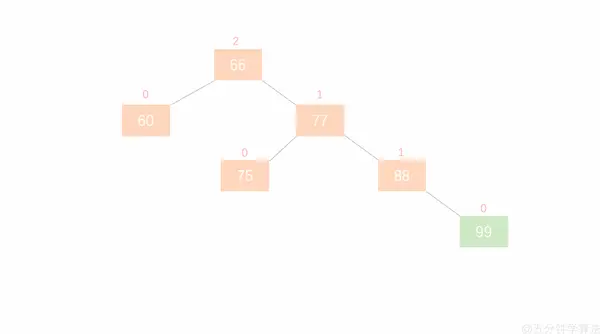
右旋

• 左高右低，BF > 0 ，右旋调整

• 右旋步骤：

  1. 节点的左孩子代表此节点

  2. 节点的左孩子的右子树变为节点的左子树

  3. 将此节点作为左孩子节点的右子树

     

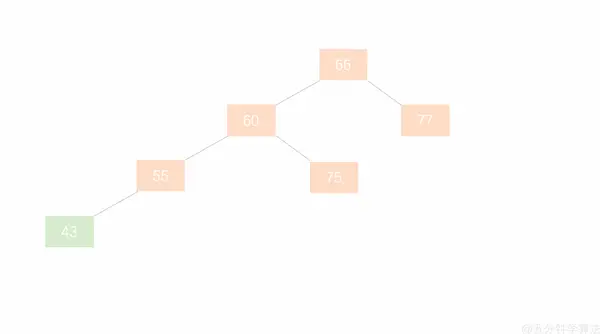
插入节点

• AVL 插入新节点后如果破坏了树的平衡结构，需要做自平衡操作
• 哪些插入情况可能造成不平衡？
  • 4种情况
• 注意：这4种情况不一定造成不平衡，只是”可能造成“

LL: A的左孩子的左孩子上插入节点

• 此时自平衡的方法为：1次右旋

RR: A的右孩子的右孩子上插入节点

• 此时自平衡的方法为：1次左旋
• 左右是相对的，LL 和 RR左右对称而已

LR: A的左孩子的右孩子上插入节点

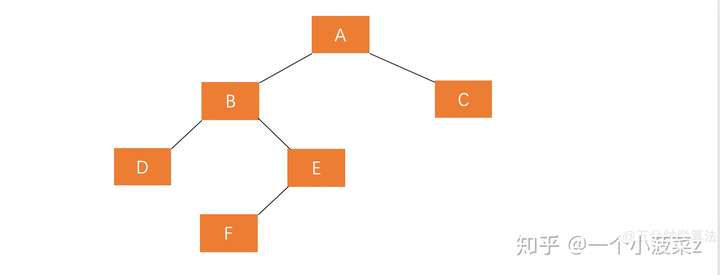
• 平衡方法：先左旋再右旋
• 1. 对失衡节点A的左孩子进行左旋转

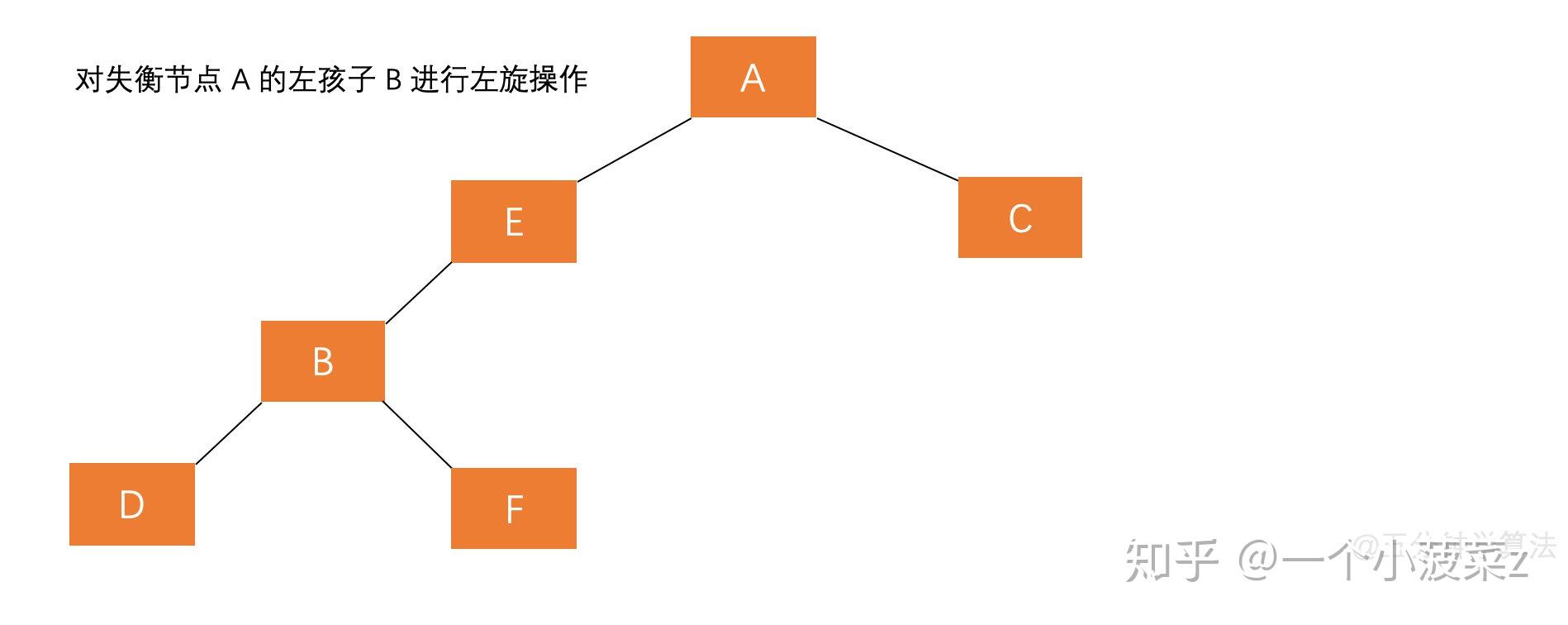
• 1. 然后再对节点A右旋

  

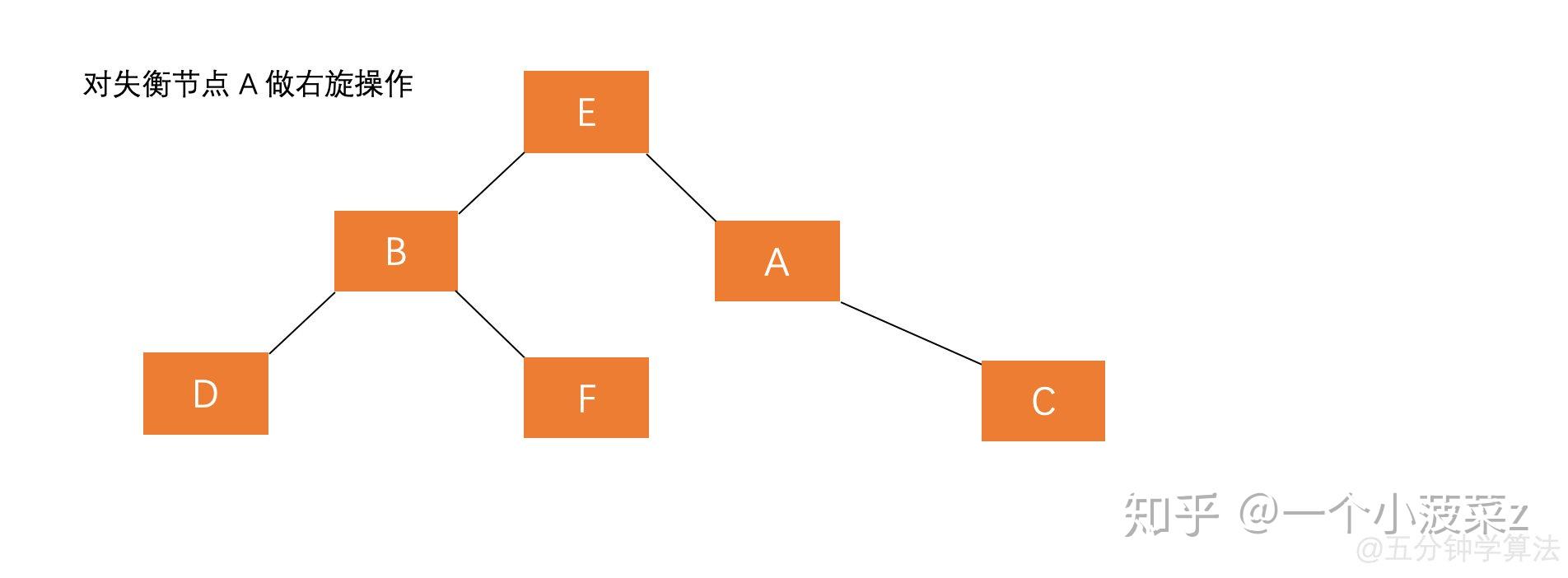
RL: A的右孩子的左孩子上插入节点

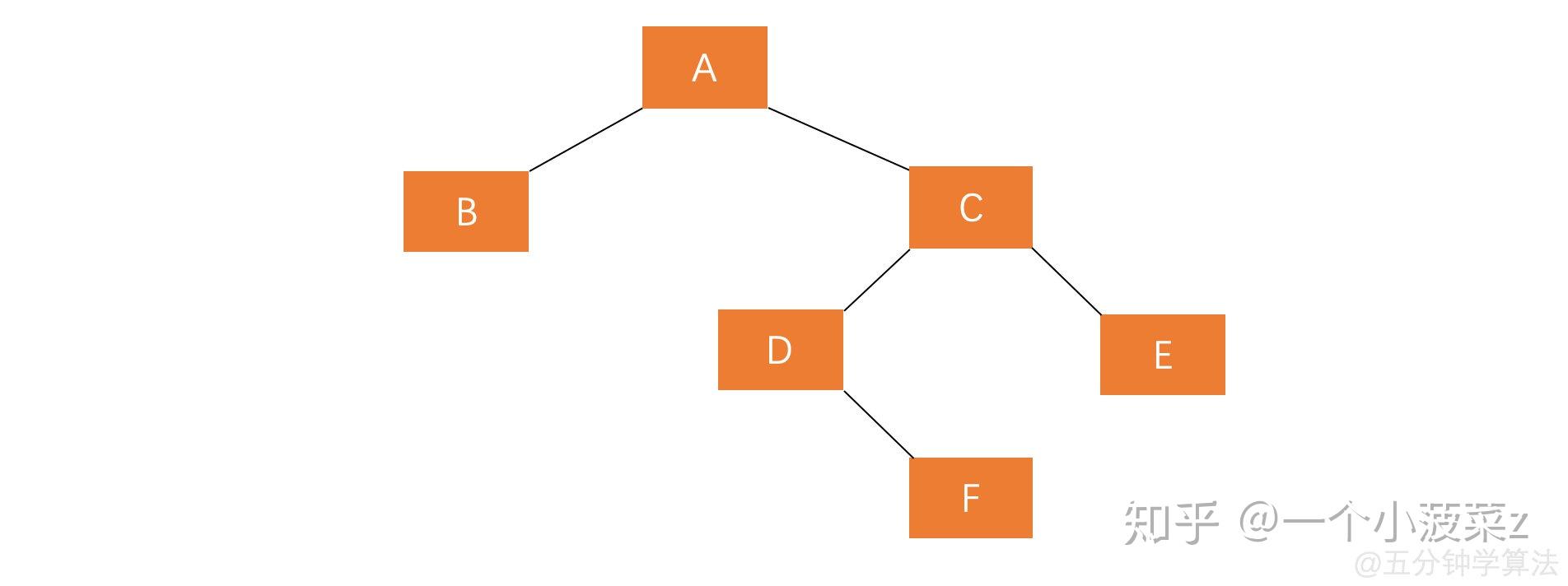
• 平衡方法：先右旋再左旋

• 1. 对失衡节点A的右孩子进行右旋操作
  2. 对失衡节点A左旋

  

总结：AVL的自平衡步骤

1. 寻找最小不平衡子树
2. 判断所属的不平衡类别（4类LL，LR，RR，RL）
3. 按照每种类别的固定程序操作即可

删除节点

四种情况

AVL 树和二叉查找树的删除操作情况一致，都分为四种情况：

• 删除叶子节点
• 删除的节点只有左子树
• 删除的节点只有右子树

• 删除的节点既有左子树又有右子树

• 只不过 AVL 树在删除节点后需要重新检查平衡性并修正，同时，删除操作与插入操作后的平衡修正区别在于，插入操作后只需要对插入栈中的弹出的第一个非平衡节点进行修正，而删除操作需要修正栈中的所有非平衡节点。

删除操作的大致步骤

1. 以前三种情况为基础尝试删除节点，并将访问节点入栈。
2. 如果尝试删除成功，则依次检查栈顶节点的平衡状态，遇到非平衡节点，即进行旋转平衡，直到栈空。
3. 如果尝试删除失败，证明是第四种情况。这时先找到被删除节点的右子树最小节点并删除它，将访问节点继续入栈。
4. 再依次检查栈顶节点的平衡状态和修正直到栈空。

• 对于删除操作造成的非平衡状态的修正，可以这样理解：对左或者右子树的删除操作相当于对右或者左子树的插入操作，然后再对应上插入的四种情况选择相应的旋转就好了。

Contact

Feel free to contact me windmillyucong@163.com anytime for anything.

License

Creative Commons BY-SA 4.0

• Previous
  RPC 通信框架
• Next
  2-3树