2-3 tree

• 2-3 树
  • Basic Concepts
    • 二叉树
    • 有序二叉树
    • 平衡二叉树
    • 2-3 树
  • 定义
    • 2-3树的定义
    • 2-3树的性质
  • 节点结构
  • 2-3树查找
  • 2-3树插入
    • 插入的4种情况
    • 向 2- 节点中插入新节点
    • 向一棵只含 一个 3- 节点的树中插入新节点
    • 向一个父节点为2-节点的3-节点中插入新节点
    • 向一个父节点为3-节点的3-节点中插入新节点
  • 2-3 树删除
    • 删除的4种情况
    • 删除非叶子节点
    • 删除3-叶子节点中的键
    • 删除2-叶子节点的键 （复杂复杂）
      • 当前待删节点的父节点是2-节点，兄弟节点是3-节点
      • 当前待删节点的父节点是2-节点，兄弟节点是2-节点
      • 当前待删节点的父节点为3-节点（复杂）
      • 2-3树为满二叉树，删除叶子节点
  • Contact
  • License

2-3 树

Created 2021.04.09 by William Yu; Last modified: 2021.04.09-V1.0.2

Contact: windmillyucong@163.com

Copyleft! 2021 William Yu. Some rights reserved.

References

• https://zhuanlan.zhihu.com/p/92394224
• https://zhuanlan.zhihu.com/p/137076341 python Code
• https://github.com/infinityglow/Algorithm-and-Complexity/blob/master/Transform%20and%20Conquer/Two-Three%20Tree/2-3%20tree.py python code
• https://www.cs.usfca.edu/~galles/visualization/Algorithms.html 算法可视化

Basic Concepts

二叉树

有序二叉树

• 有序二叉树的缺点：
  • 当原序列本身就有序时，搜索效率降低为O(n)

平衡二叉树

• 为解决有序二叉树的搜索效率低的问题，使用平衡二叉树维护树的高度
• 性能消耗：每次插入与删除节点后，需要维护树的平衡

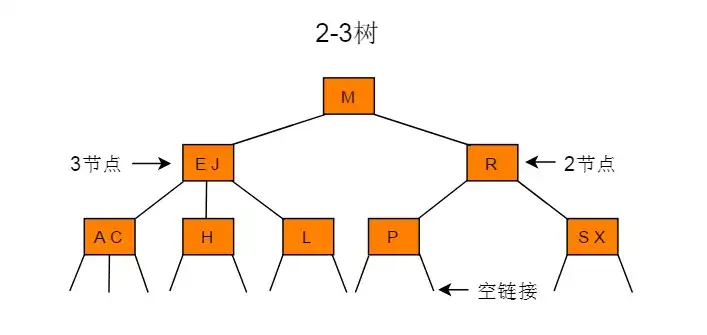
2-3 树

• 2-3树本质也是一种平衡搜索树，但不是二叉树
• 2-3树可以有两种节点：
  • 2-节点：拥有一个键和两个子节点
  • 3-节点：拥有两个键和三个子节点

定义

2-3树的定义

• 2-3树可以为空
• 2-节点有一个数据域和两个子节点
  • 当前节点的数值大于左子树中所有节点的数据，小于右子树中所有节点的数据
• 3-节点有两个数据域和三个子节点
  • 左子树中所有节点的数据要小于a
  • 中子树中所有节点的数据要大于a小于b
  • 右子树中所有节点的数据要大于b

2-3树的性质

• 所有叶子节点都在树的同一层
• 上面这一条性质是需要维护的

节点结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
template <class T>
class TwoThreeNode {
public:
    // 数据域
    T data1;                    // 第一个数据
    T data2;                    // 第二个数据（仅3-节点使用）
    
    // 指针域
    TwoThreeNode* left;         // 左子树
    TwoThreeNode* middle;       // 中子树
    TwoThreeNode* right;        // 右子树
    TwoThreeNode* parent;       // 父节点
    
    // 节点类型标识
    bool is_two_node;           // true表示2-节点，false表示3-节点
    
    // 构造函数
    TwoThreeNode() : left(nullptr), middle(nullptr), right(nullptr), 
                     parent(nullptr), is_two_node(true) {}
    
    TwoThreeNode(T value) : data1(value), left(nullptr), middle(nullptr), 
                           right(nullptr), parent(nullptr), is_two_node(true) {}
    
    TwoThreeNode(T value1, T value2) : data1(value1), data2(value2), 
                                      left(nullptr), middle(nullptr), 
                                      right(nullptr), parent(nullptr), 
                                      is_two_node(false) {}
    
    // 判断是否为叶子节点
    bool is_leaf() const {
        return left == nullptr && middle == nullptr && right == nullptr;
    }
    
    // 获取节点中键的数量
    int key_count() const {
        return is_two_node ? 1 : 2;
    }
};

template <class T>
class TwoThreeTree {
private:
    TwoThreeNode<T>* root;
    
public:
    TwoThreeTree() : root(nullptr) {}
    
    // 基本操作声明
    bool search(const T& key);
    void insert(const T& key);
    void remove(const T& key);
    void inorder_traversal();
    
private:
    // 辅助函数声明
    TwoThreeNode<T>* search_helper(TwoThreeNode<T>* node, const T& key);
    TwoThreeNode<T>* insert_helper(TwoThreeNode<T>* node, const T& key);
    TwoThreeNode<T>* remove_helper(TwoThreeNode<T>* node, const T& key);
    void inorder_helper(TwoThreeNode<T>* node);
};

2-3树查找

太简单了，略过

2-3树插入

• 先查找，若已存在，则不插入

插入的4种情况

• 向 2- 节点中插入新节点
• 向一棵只含 3- 节点的树中插入新节点
• 向一个父节点为 2- 节点的 3- 节点中插入新节点
• 向一个父节点为 3- 节点的 3- 节点中插入新节点

向 2- 节点中插入新节点

1. 直接将2-节点变为3-节点，将新节点插入即可

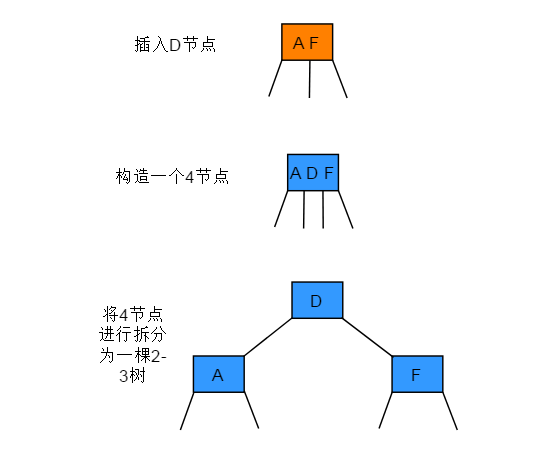
向一棵只含 一个 3- 节点的树中插入新节点

1. 先临时将新键存入唯一的3-节点中，构造一个4-节点
2. 将4-节点转化为由3个2节点组成的2-3树
3. 分解后树的高度会增加1

向一个父节点为2-节点的3-节点中插入新节点

1. 先临时将新键存入3-节点中，构造一个4-节点

2. 将该 4-节点拆分

   1. 分解时将中键移动到父节点中将，父节点由2-节点变成3-节点
      1. 该中键在父节点中的位置由它和原父节点中的键的大小决定
   2. 原4节点的左右两个键变成两个2-节点

   

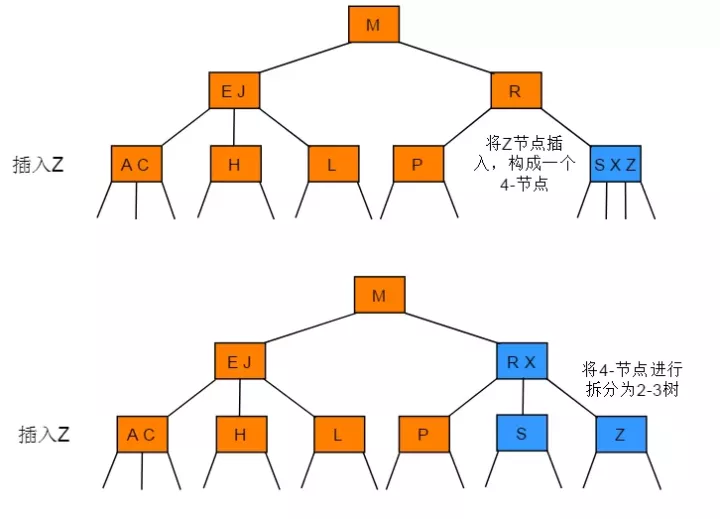
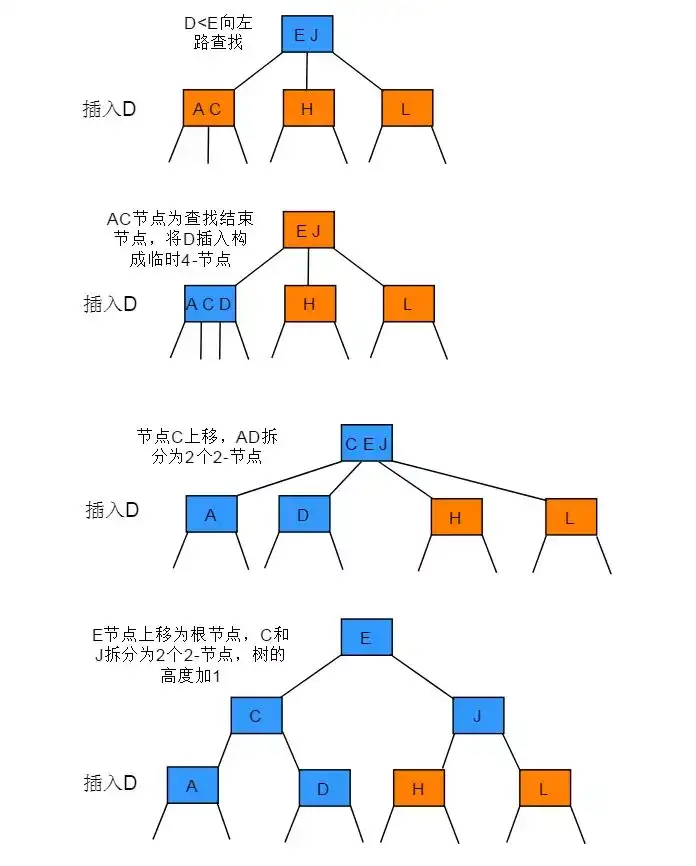
向一个父节点为3-节点的3-节点中插入新节点

1. 插入节点后构造临时4- 节点
2. 分解临时4- 节点，将中键向上合并
3. 重复上述步骤，构造4-节点，分解，向上合并
4. 直到遇到一个2-节点，并将其合并为一个不需要继续分解的3-节点
5. 或者遇到根节点
   1. 若根节点是2节点，变成3-节点即可
   2. 若根节点本身就已经是3-节点，合并新键之后，根节点变成4- 节点，需要继续分解根节点

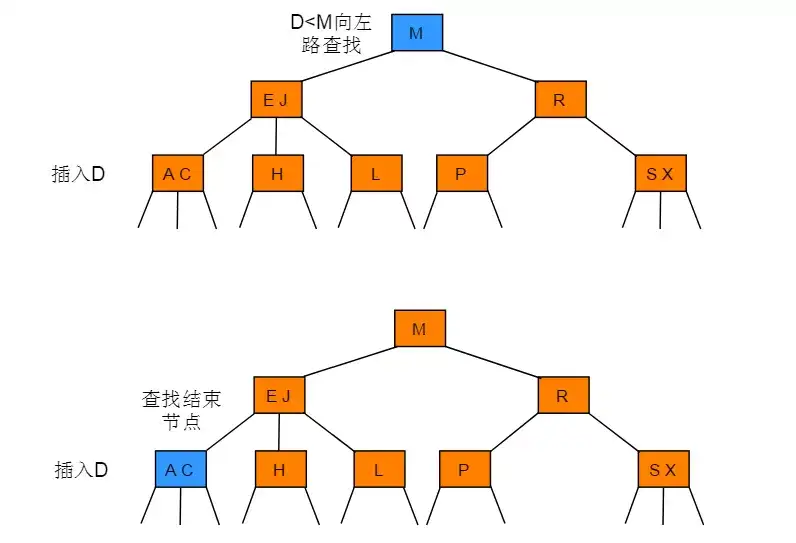
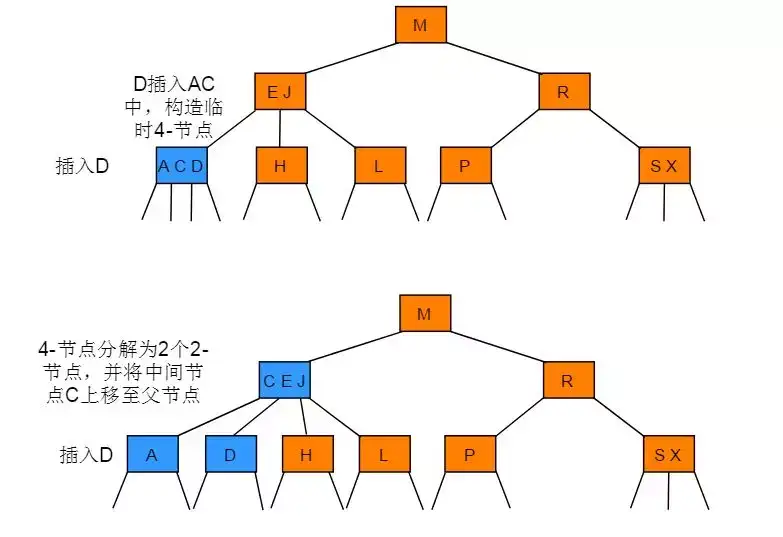
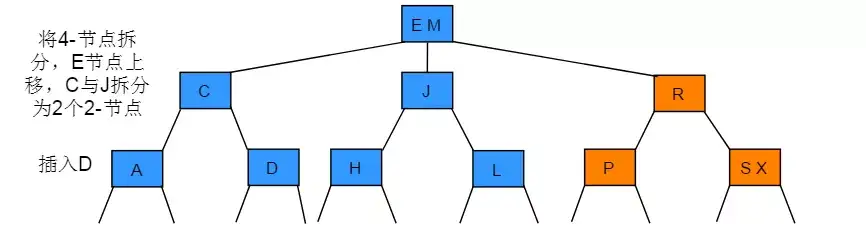
分解根节点

2-3 树删除

删除之前先查找，查找成功才可以删除

删除的4种情况

• 删除非叶子节点
• 删除不为2-节点的叶子节点
• 删除 2-节点的叶子节点

删除非叶子节点

1. 使用中序遍历下的直接后继节点key 来覆盖 当前待删节点key
2. 再删除用来覆盖的后继节点key

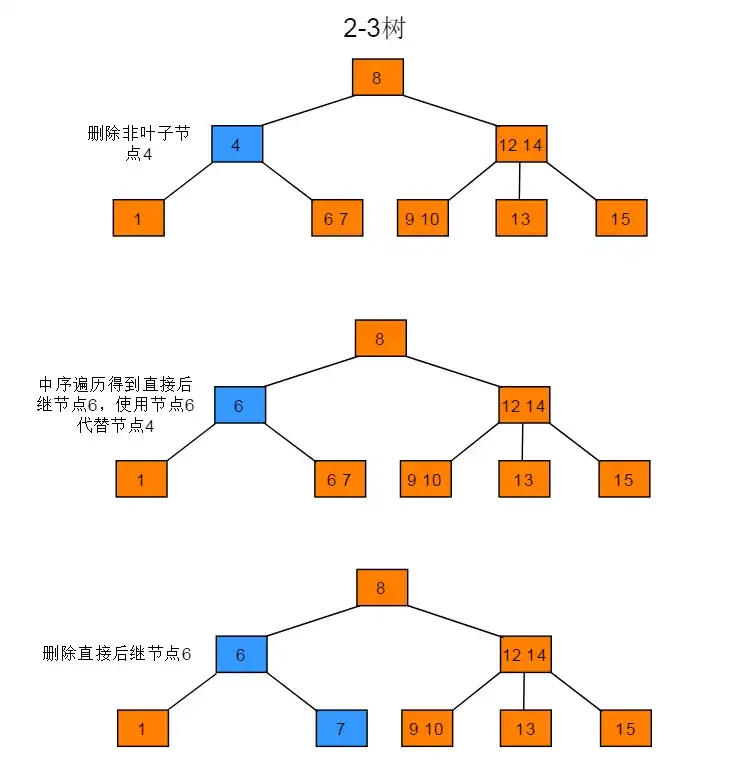
删除3-叶子节点中的键

1. 直接删除即可

   

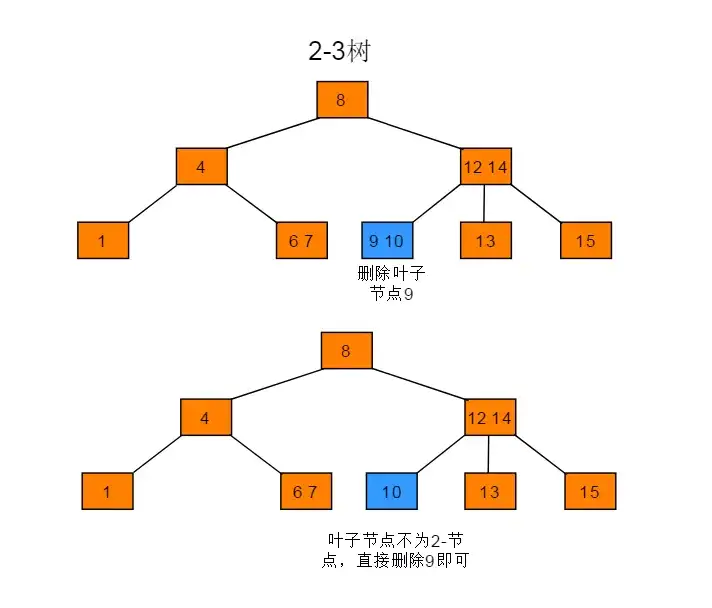
删除2-叶子节点的键 （复杂复杂）

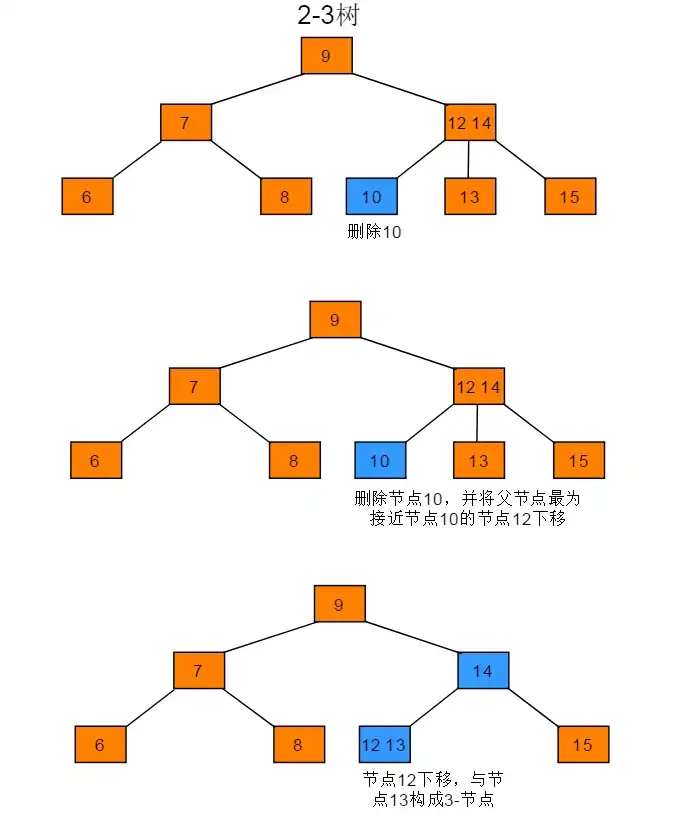
当前待删节点的父节点是2-节点，兄弟节点是3-节点

1. 将父节点移动到当前待删节点位置
2. 将兄弟节点中最接近当前位置的key移动到父节点

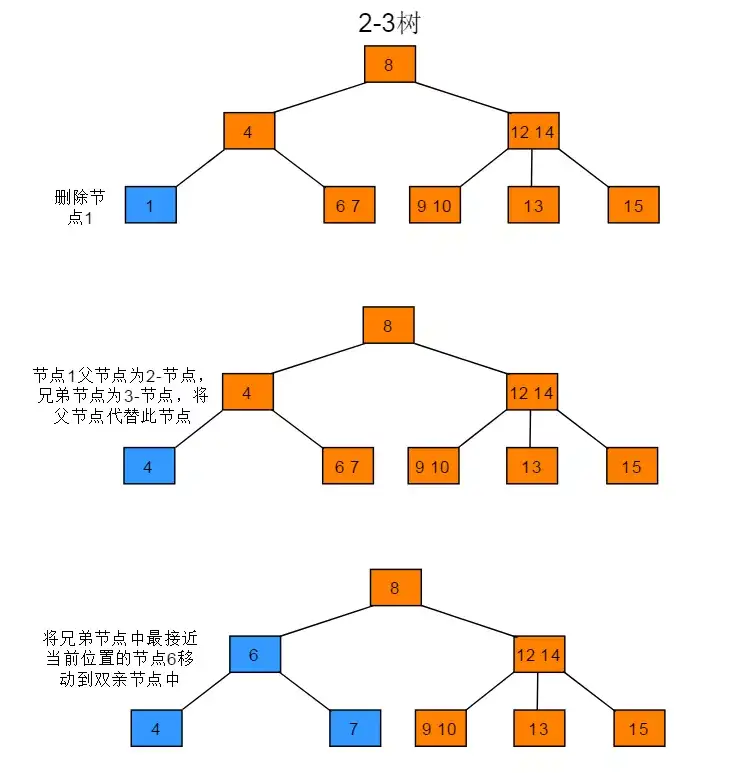
当前待删节点的父节点是2-节点，兄弟节点是2-节点

1. 移动兄弟节点的中序遍历直接后驱到兄弟节点
2. 使兄弟节点变成3-节点
3. 变成上一种情况

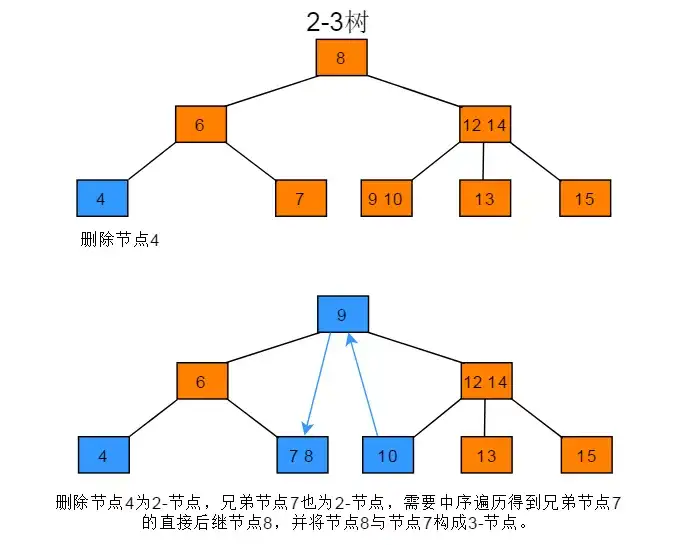
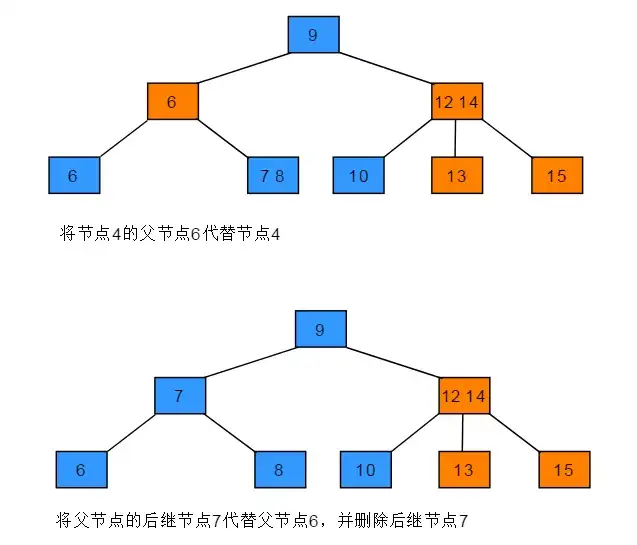
当前待删节点的父节点为3-节点（复杂）

1. 将3-父节点中的一个键移动到孩子中，父节点变成2-节点

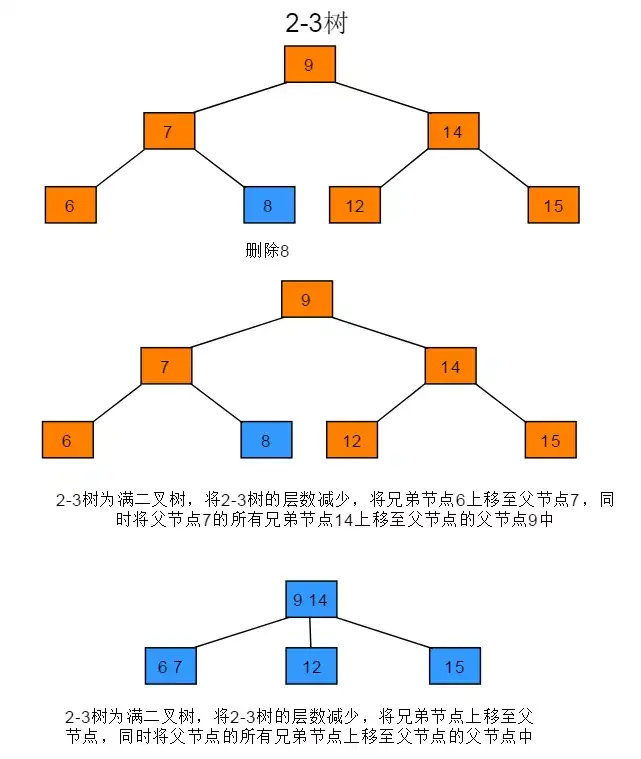
2-3树为满二叉树，删除叶子节点

1. 将2-3树的层数减少
2. 将当前删除节点的兄弟节点合并到父节点中
3. 同时将父节点的所有兄弟节点合并到父节点的父节点中
4. 如果产生了4-节点，再分解4-节点

Contact

Feel free to contact me windmillyucong@163.com anytime for anything.

License

Creative Commons BY-SA 4.0

• Previous
  平衡二叉树AVL
• Next
  B树