Bayesian Filter

• Kalman Filter
  • Basic Concepts
    • 状态方程
  • Model
    • 1.1 运动方程（状态转移方程）
    • 1.2 观测方程
    • 1.3 噪声
  • Process
    • 1. Init
    • 2. Predict
    • 3. Update
    • Process
  • Tips
• EKF
  • Model
    • 1. Similarities with KF
    • 2. Difference between KF
    • 1.1 运动方程
    • 1.2 观测方程
  • Process
    • 1. Init
    • 2. Predict
    • 3. Update

---

Created 2021.05.16 by William Yu; Last modified: 2022.07.12-V1.2.2

Contact: windmillyucong@163.com

Copyleft! 2022 William Yu. Some rights reserved.

---

Kalman Filter

卡尔曼滤波（Kalman filter）1960.

refitem:

• paper https://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf
• blog https://zhuanlan.zhihu.com/p/39912633
• blog https://longaspire.github.io/blog/%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2/
• blog https://zhuanlan.zhihu.com/p/48876718
• blog 关于协方差矩阵 https://zhuanlan.zhihu.com/p/338335181

Basic Concepts

• $(\check.)$ 表示先验

• $(\hat.)$ 表示后验（即最佳估计值）

• 高斯白噪声
  • 符合高斯分布
• 基本模型
  • 马尔科夫链
• 基本过程，包括两个阶段：
  • 预测阶段
    • 使用上一状态的估计，做出对当前状态的估计
  • 更新阶段
    • 使用对当前状态的观测值优化之前在预测阶段获得的预测值，获得更精确的估计值
• 特点
  • 适合不断变化的系统，时变系统
  • 内存占用较小（只需保留前一个状态）
  • 速度快

状态方程

$$\vec x_k ： (\vec p,\vec v)$$

• 状态 $\vec x$ 由两部分组成
• $\vec x$ 的实际值并不知
• 卡尔曼滤波假设每个变量（在我们的例子里是位置和速度）都应该是随机的，而且符合高斯分布。每个变量都有一个均值 $\mu$ ，它是随机分布的中心；有一个方差$\sigma^2$
• 这些输入信息可能是相关的，也可能不是相关的

• 协方差矩阵

Model

1.1 运动方程（状态转移方程）

系统的状态转移方程（运动方程），线性方程 $x_k = A \cdot x_{k-1} + B \cdot u_{k} + w_{k} \tag1$

• where：
  • $x_k$ ： k时刻的运动模型预估的系统状态
  • $u_k$ ：k时刻对系统的控制量
  • A ：转移矩阵，运动模型
  • B：系统参数
  • $w_k$：过程激励噪声

1.2 观测方程

$$z_k = H \cdot x_k + v_k \tag2$$

• where：

  • $z_k$：k时刻的观测值
  • H：观测系统的参数
  • $v_k$：观测过程的噪声

1.3 噪声

$$\begin{align} p(w) ∼ N (0, Q) \\ p(v) ∼ N (0, R) \end{align}$$

• 随机信号 w(k) 和 v(k) 分别表示运动噪声和观测噪声
• 假设它们为相互独立，正态分布的白色噪声
• 实际系统中，这QR可能会随着每次迭代计算而发生变化，但此处假设他们是常量

Process

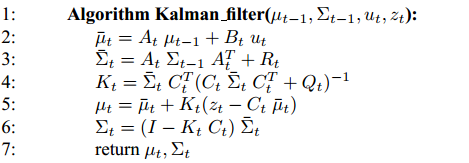
1. Init

2. Predict

状态转移：由运动方程做先验估计 $x_k^- = A \cdot x_{k-1} + B \cdot u_{k} \tag3$ 协方差转移 $P_k^- = A \cdot P_{k-1} \cdot A^T + Q \tag4$

3. Update

计算卡尔曼增益（中间量） $K_k = P_k^- H^T (HP_k^-H^T + R )^{-1} \tag 5$ 状态更新 $x_k := x_k^- + K_k(\underbrace{ z_k - \underbrace{H x_k^-}_{\rm measure} }_{\rm error}) \tag 6$ 协方差更新 $P_k := (I - K_k H)P_k^- \tag 7$

Process

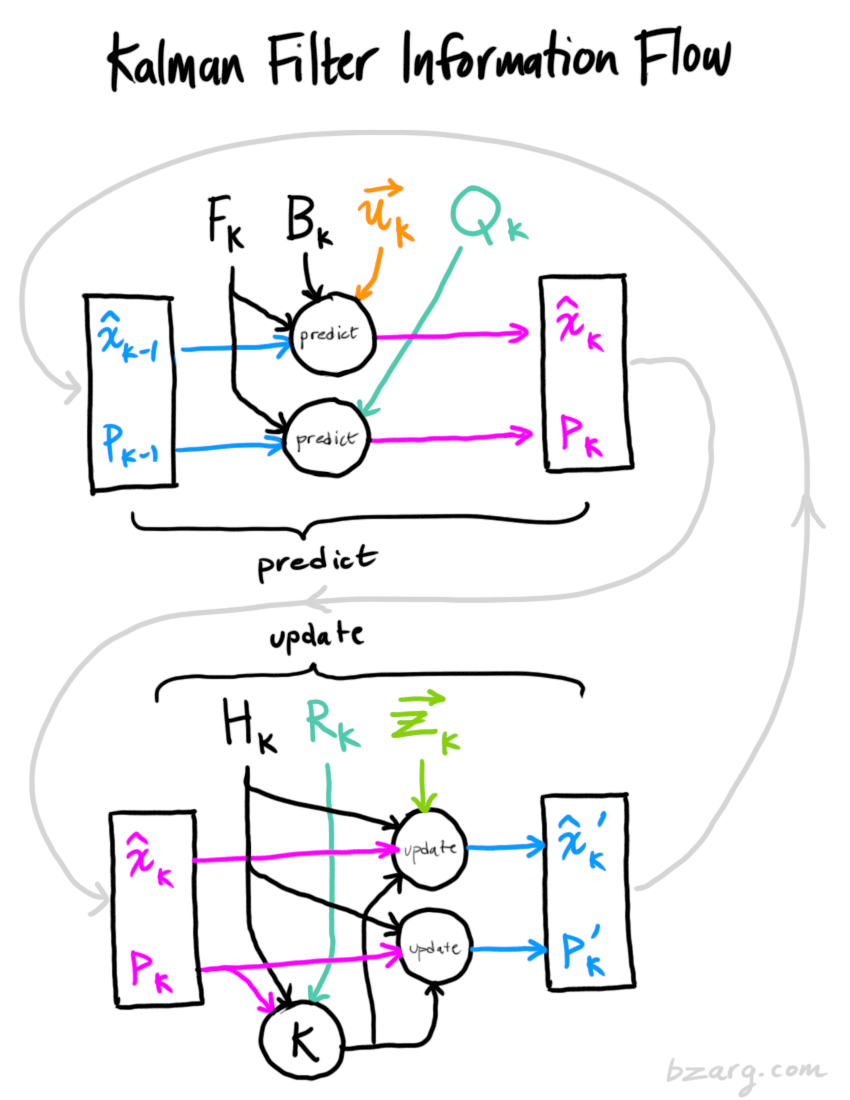
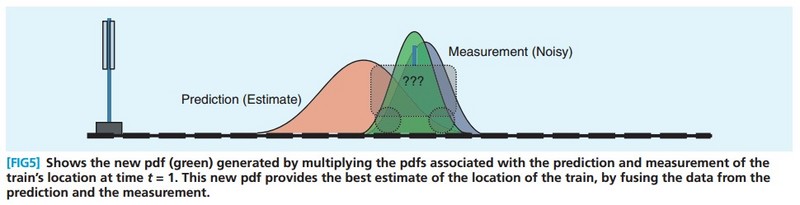
Tips

1. Kalman filter defines every state with Guissian $(\eta, \sigma^2)$.

   Kalman filter predicts and updates not only $\eta$, but also $\sigma$.

   While Bayesian filter only offer a $\eta$

2. What is K for? 卡尔曼增益是干啥用的？

   // todo(congyu)

EKF

Extended Kalman filter（扩展卡尔曼滤波，EKF）

refitem:

• introductory paper https://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf

Model

1. Similarities with KF

1. 状态量服从正态分布

1. 观测量服从正态分布

1. 过程噪声服从均值为 0 的正态分布

1. 观测噪声服从均值为 0 的正态分布

2. Difference between KF

1. EKF中 状态转移函数和（或）观测函数为非线性函数
   • 在卡尔曼滤波的前提假设中，认为状态方程中的状态转移函数 以及观测方程中的测函数 均为线性函数。
   • 基于这种线性假设，存在常数或常矩阵 ，使得 可以写成卡尔曼滤波中的线性形式，存在常数或常矩阵 ，使得 也可以写成卡尔曼滤波中的线性形式。
   • 不同于标准卡尔曼滤波，扩展卡尔曼滤波处理的是非线性系统，假设系统的状态转移函数和（或）观测函数为非线性函数。

扩展卡尔曼滤波的处理方法非常简单：将非线性方程一阶泰勒展开成线性方程：

1.1 运动方程

$$x_k = f ( x_{k-1}, u_{k}) + w_{k} \tag8$$

非线性方程线性化 $x_k^- = f ( x_{k-1}, u_{k}, 0) \tag9 \\ F_{k-1} = \frac {\partial f(x_{k-1}, u_k, w_k) }{\partial x_{k-1} } | _{x_{k-1}, u_k,0}$

1.2 观测方程

$$z_k = h ( x_k) + v_k \tag{10}$$

非线性方程线性化 $z_k = h(x_k, 0) \tag{11} \\ H_k = \frac{\partial h(x_k,v_k)}{\partial x_k} | _{x_{k}, 0}$

Process

Notice: 图中箭头所指的非线性函数！是与卡尔曼滤波的区别,图中的g即本文档中的f.

1. Init

2. Predict

$$x_k^- = f(x_{k-1}, u_{k-1},0) \tag {12}$$ $$P_k^- = F_{k}P_{k-1}F_{k}^T + Q \tag{13}$$

3. Update

$$K_k = P_k^- H_k^T (H_kP^-_kH_k^T + R )^{-1} \tag {14}$$ $$x_k := x_k^- + K_k(z_k - h(x_k^-,0)) \tag {15}$$ $$P_k := (I-K_kH_k)P_k^-\tag{16}$$

---

• Previous
  Bayesian Filter
• Next
  Error-State Kalman Filter

---