DEMO

Euler Angles

Created 2021.06.02 by Cong Yu; Last modified: 2021.06.02-v1.0.2

Contact: windmillyucong@163.com

Copyleft! 2022 Cong Yu. Some rights reserved.

Euler Angles

References

wolfram post https://mathworld.wolfram.com/EulerAngles.html
MIT courseware KINEMATICS OF MOVING FRAMES
post https://hideoninternet.github.io/2020/02/17/36f31d81/
post https://blog.csdn.net/weixin_42927959/article/details/89880825
post https://zhuanlan.zhihu.com/p/85108850
blog 欧拉角微分方程的推导
book 惯性导航, 秦永元，p288.

约定

robot坐标系 front x, left y, up z
欧拉角顺序 zyx ypr yaw pitch roll
$\Psi$ 方向或偏航 (heading or yaw)
$\theta$ 升降或俯仰 (elevation or pitch)
$\phi$ 倾斜或横滚 (bank or roll)
n系导航坐标系
b系机体坐标系

1. 基本概念

欧拉角有三个要素：

规定顺序
- 本文约定 // the euler angle sequence (zyx, ypr, z->y->x, yaw->pitch->roll)
规定内旋外旋
- 内旋
  - 也称为静态欧拉角
  - 每次旋转都是绕全局固定轴，即世界坐标系的轴旋转
- 外旋
  - 也称为动态欧拉角
  - 每次旋转都是绕上一次旋转之后的轴
- 通常使用的是动态欧拉角。本博客只讨论常用的动态欧拉角。
角度数值
- 使用三个参数表达三维姿态 [yaw,pitch,roll]。数值范围都是-180°到+180°

2. 表达姿态

欧拉角表达姿态时并不唯一。三维中的任一姿态，都可以有至少两个欧拉角表达，第二个等于第一个减去180°。
比如：姿态1（10°，20°，110°）等同于姿态2（-170°，-160°，-70°）

3. 表达旋转

表达姿态间的旋转动作时，直接做差即可。
比如：姿态1 （12°，100°，113°），姿态2（15°，108°，117°），这两个姿态之间的旋转动作为（3°，8°，4°）
表达逆旋转，直接三个数字上加负号即可。
比如：任意姿态，叠加旋转1（12°，100°，113°），再叠加旋转2（-12°，-100°，-113°），就会回到该姿态不变。
表达旋转叠加时，直接求和即可。
比如：旋转1（12°，100°，113°），再叠加旋转2（-12°，-100°，-113°）,总的旋转等于两者数值直接相加。

4. 万向锁 gimbal lock

理解万向锁需要注意以下关键点：（注意！下面这一部分理解透彻是非常重要的）

第一个关键点：注意欧拉角的旋转轴并不是正交的，从桁架系统这个机构去理解：
- z轴其实永远是朝向正上方的
- y轴其实永远在水平面里面
- x轴可以出现在空间中的任意位置，但他永远在垂直于当时的y轴，在垂直于当时的yz轴平面的竖直平面里面
第二个关键点：理解万向锁，是要用delta_theta或者说多次旋转或者说从欧拉角微分的思路来理解自由度丢失和锁的概念的！！！
- 或者说是从用欧拉角表达旋转而不是从用欧拉角表达姿态这件事情来理解锁这个字。
- 为什么一定是从转动的角度来思考？举个例子：相机的拍摄时候的运镜，游戏中人物的手臂的运动。
- 我们需要的是：在任何一个姿态下，可以向任何另外一个姿态过渡。但是在万向锁姿态下，只有两个方向是可以微分的（围绕y轴的微分 + 围绕xz轴的这两个重叠的微分）
第三个关键点：注意理解欧拉角的顺序。
- 并不是说必须按照顺序依次做三个旋转，顺序颠倒也是可以的，但是注意耦合关系。
- 先转哪个轴都可以，但是要确保确保转z轴的时候xy都会被带动，转y轴的时候x轴会被带动，转x轴的时候其他不动即可。
- 与其说是欧拉角顺序，不如说是欧拉角父子关系。这个父子关系也正是桁架系统的物理安装结构。

euler_angle_description.excalidraw

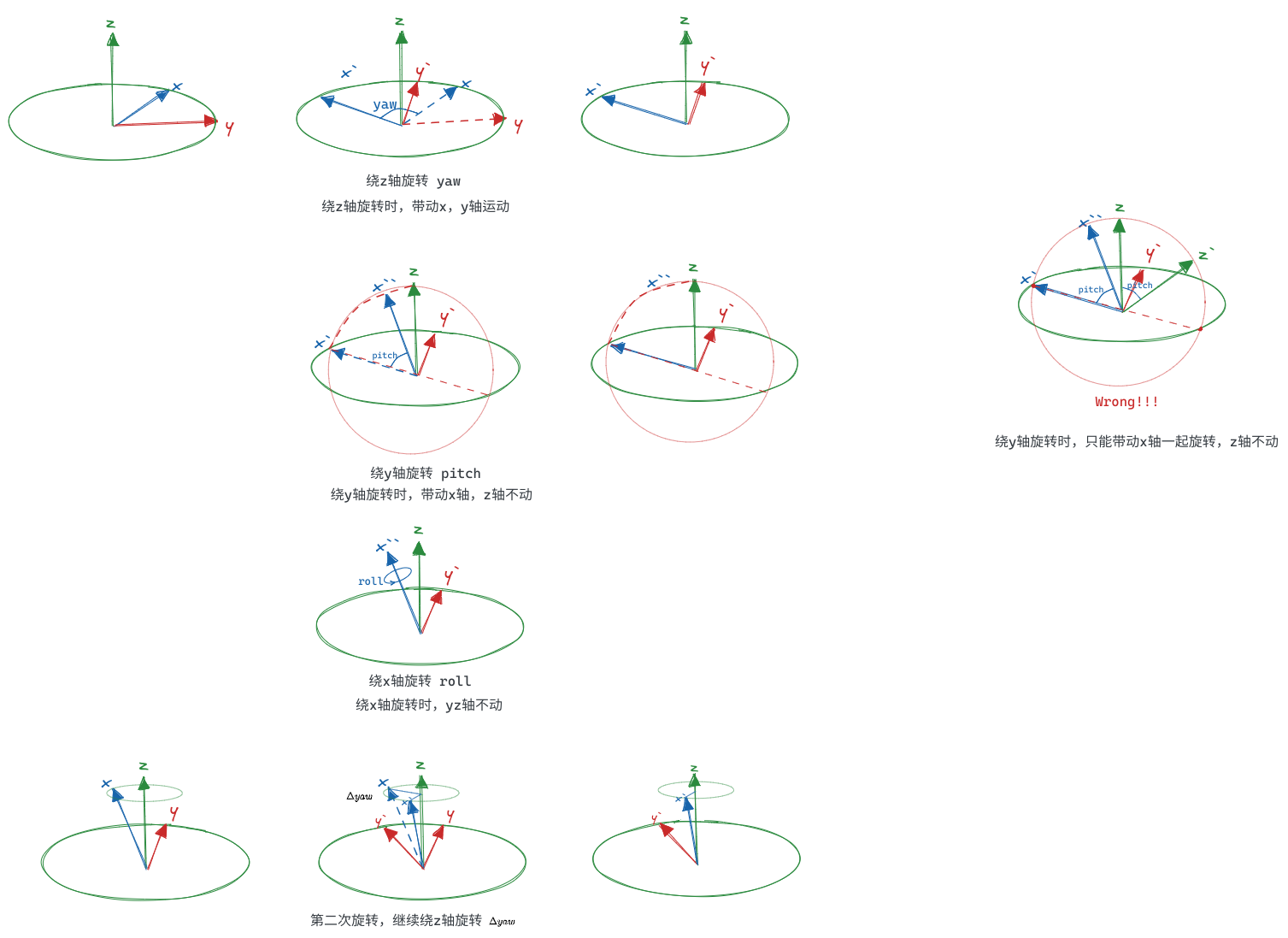
x与z重合时，绕z旋转等效于绕x旋转，就产生了万向锁。

5. 欧拉角表达下的陀螺仪积分

Gyro Integration with Euler Angles

5.1. 欧拉角微分推导

Derivations

某姿态 $R_n^b = R_2^b(\phi) \cdot R_1^2(\theta) \cdot R_n^1(\psi) \tag1$

其中$R_n^b$表示从n系（导航系）到b系（机体系）的旋转动作。

注意欧拉角微分$w_e$并不等于陀螺仪的角速度测量值$w_b$ $\begin{gather} w_e \equiv \left[ \begin{matrix} {\dot\psi} \ {\dot\theta}\ {\dot\phi} \end{matrix} \right]^T \\ w_b \equiv \left[ \begin{matrix} w_{z} \ w_{y} \ w_{x} \end{matrix} \right]^T \\ w_n \not= w_b \end{gather}$

原因：动态欧拉角的轴并不一定正交，是由当前姿态决定的。而IMU的瞬时测量值是在I系下测得的，是正交的。只有旋转轴和角速度轴重合的情况下才能积分。所以角速度需要被投影分解到相应的欧拉角旋转轴上面去才能积分。

可以理解为I系是附着在欧拉角桁架系统的x轴上的！

5.2. 投影步骤

Step 1. yaw旋转:旋转轴为$Z_n$轴，因此 $w_{bz} = R_2^b(\phi) \cdot R_1^2(\theta) \cdot \left[ \begin{matrix} {\dot\psi} \ 0 \ 0 \end{matrix} \right]^T \tag{2}$ Step 2. pitch旋转:旋转轴是做完yaw旋转之后的机体$Y_1$, $w_{by} =R_2^b(\phi) \cdot\left[ \begin{matrix} 0 \ {\dot\theta} \ 0 \end{matrix} \right]^T \tag3$ Step 3. roll旋转:旋转轴是做完前两次旋转之后的机体$X_2$轴，也是最终的IMU的x轴，旋转轴重合，因此直接有 $w_{bx} =\left[ \begin{matrix} 0 \ 0 \ \dot\phi \end{matrix} \right]^T \tag{4}$ 于是有 $w_b = w_{bz} + w_{by} + w_{bx} \\ = R^b_{\dot\psi \dot\theta \dot\phi} w_n \tag5$

则可以求出$w_e$

\[w_e = (R^b_{\dot\psi \dot\theta \dot\phi}) ^ {-1} w_b \tag6\]

然后对$w_e$积分即可得到正确的欧拉角。

5.3. 投影步骤-借助$w_n$

注意到，上述投影步骤，理解起来并不容易。可以有借助$w_n$的推导：

\[\begin{gather} \\ w_b = R_2^bR_1^2R_n^1 w_n \\ \dot \psi = R_n^1 w_{nz} = R_n^1 R_1^n R_2^1 R_b^2 w_{bz} = R_2^1 R_b^2 w_{bz} \\ \dot \theta = R_1^2 R_n^1 w_{ny} = R_1^2 R_n^1 R_1^n R_2^1 R_b^2 w_{by} = R_b^2 w_{by} \\ \dot \phi = R_2^b R_1^2 R_n^1 w_{nx} = R_2^b R_1^2 R_n^1R_1^n R_2^1 R_b^2 w_{bx} = w_{bx} \end{gather}\]

特别注意

${\dot\psi} \ {\dot\theta}\ {\dot\phi}$ 在n系下并不正交，所以积分区间必须足够小。
万向锁：$\theta = ±90°$的时候，${\dot\psi} \ 与\ {\dot\phi}$ 旋转轴重合，丧失一个自由度，yaw和roll有无穷多解，故不可用于全角度姿态解算。

三维刚体运动基础系列之欧拉角!

欧拉角姿态表达，以及欧拉角微分推导