本文主要整理总结 空间位姿表达方式之间的相互转换,包括原理与数学公式,以及代码实现,以及几何库的使用。
Created 2021.06.10 by Cong Yu; Last modified: 2021.06.10-v1.0.2
Contact: windmillyucong@163.com
Copyleft! 2022 Cong Yu. Some rights reserved.
Geometry-Convert
References
python的旋转库
- https://matthew-brett.github.io/transforms3d/reference/transforms3d.euler.html
-
https://zhuanlan.zhihu.com/p/526354689
- https://zhuanlan.zhihu.com/p/362410159
- https://blog.csdn.net/xiaoma_bk/article/details/79082629
- https://krasjet.github.io/quaternion/quaternion.pdf
- https://krasjet.github.io/quaternion/bonus_gimbal_lock.pdf
- https://blog.csdn.net/u011092188/article/details/77430988
注意:若未特殊说明,本文中的欧拉角顺序均定义为Euler sequence: yaw (z), pitch (y), roll (x) zyx ypr yaw,pitch,roll
1. 表达方式
- 欧拉角
- 四元数
- 轴角
- 旋转矩阵
2. 计算库
- c++ Eigen
- Python transform3d
- OpenCV
- PCL
3. 使用Eigen的相互转换
头文件
1
2
3
4
#include <glog/logging.h>
#include <Eigen/Core>
#include <Eigen/Geometry>
转换函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
namespace pose {
/******************************************* 欧拉角 ************************/
/**
* @brief Euler2Quaternion 欧拉角 -> 四元数
* @param euler_angle
* Euler sequence: z->y->x zyx ypr yaw,pitch,roll
* 注意:定义的Euler角顺序一定要一致
* @retval Eigen::Quaterniond
*/
Eigen::Quaterniond Euler2Quaternion(const double yaw, const double pitch,
const double roll) {
Eigen::AngleAxisd yaw_angleax(yaw, Eigen::Vector3d::UnitZ());
Eigen::AngleAxisd pitch_angleax(pitch, Eigen::Vector3d::UnitY());
Eigen::AngleAxisd roll_angleax(roll, Eigen::Vector3d::UnitX());
Eigen::Quaterniond q = yaw_angleax * pitch_angleax * roll_angleax;
LOG(ERROR) << "Euler2Quaternion result is:\n"
<< "w,x,y,z = [" << q.w() << "," << q.x() << "," << q.y() << ","
<< q.z() << "]";
return q;
}
/**
* @brief Euler2RotationMatrix 欧拉角 -> 旋转矩阵
* @param euler_angle
* Euler sequence: z->y->x zyx ypr yaw,pitch,roll
* 注意:定义的Euler角顺序一定要一致
* @retval Eigen::Matrix3d RotationMatrix
*/
Eigen::Matrix3d Euler2RotationMatrix(const double yaw, const double pitch,
const double roll) {
Eigen::AngleAxisd yaw_angleax(yaw, Eigen::Vector3d::UnitZ());
Eigen::AngleAxisd pitch_angleax(pitch, Eigen::Vector3d::UnitY());
Eigen::AngleAxisd roll_angleax(roll, Eigen::Vector3d::UnitX());
Eigen::Quaterniond q = yaw_angleax * pitch_angleax * roll_angleax;
Eigen::Matrix3d rotation_matrix = q.matrix();
LOG(ERROR) << "Euler2RotationMatrix result is:\n"
<< "rotation_matrix = \n"
<< rotation_matrix;
return rotation_matrix;
}
/**
* @brief Euler2AngleAxis 欧拉角 -> 轴角
* @param euler_angle
* Euler sequence: z->y->x zyx ypr yaw,pitch,roll
* 注意:定义的Euler角顺序一定要一致
* @retval Eigen::AngleAxisd
*/
Eigen::AngleAxisd Euler2AngleAxis(const double yaw, const double pitch,
const double roll) {
Eigen::AngleAxisd yaw_angleax(yaw, Eigen::Vector3d::UnitZ());
Eigen::AngleAxisd pitch_angleax(pitch, Eigen::Vector3d::UnitY());
Eigen::AngleAxisd roll_angleax(roll, Eigen::Vector3d::UnitX());
Eigen::AngleAxisd angle_axis;
angle_axis = yaw_angleax * pitch_angleax * roll_angleax;
LOG(ERROR) << "Euler2AngleAxis result is:\n"
<< "rvec:axis:[" << angle_axis.axis().transpose()
<< "] ,angle(rad):" << angle_axis.angle();
return angle_axis;
}
/******************************************* 四元数 ************************/
/**
* @brief Quaternion2Euler 四元数 -> 欧拉角
* @param Quaternion(x-i, y-j, z-k, w) 前三个虚部,最后一个实部
* @retval Eigen::Vector3d euler_angle
* Euler sequence: z->y->x zyx ypr yaw,pitch,roll
*/
Eigen::Vector3d Quaternion2Euler(const double x, const double y, const double z,
const double w) {
Eigen::Quaterniond q;
q.x() = x;
q.y() = y;
q.z() = z;
q.w() = w;
// or Eigen::Quaterniond q(w, x, y, z); // 注意构造时第一个数字是w
// Euler sequence: z->y->x zyx ypr yaw,pitch,roll
Eigen::Vector3d euler = q.toRotationMatrix().eulerAngles(2, 1, 0);
LOG(ERROR) << "Quaternion2Euler result is:\n"
<< "z,y,x|yaw,pitch,roll = [" << euler[0] << "," << euler[1] << ","
<< euler[2] << "]";
return euler;
}
/**
* @brief Quaternion2RotationMatrix 四元数 -> 旋转矩阵
* @param Quaternion(x-i, y-j, z-k, w) 前三个虚部,最后一个实部
* @retval Eigen::Matrix3d
*/
Eigen::Matrix3d Quaternion2RotationMatrix(const double x, const double y,
const double z, const double w) {
Eigen::Quaterniond q;
q.x() = x;
q.y() = y;
q.z() = z;
q.w() = w;
// or Eigen::Quaterniond q(w, x, y, z); // 注意构造时第一个数字是w
Eigen::Matrix3d rotation_matrix = q.normalized().toRotationMatrix();
LOG(ERROR) << "Quaternion2RotationMatrix result is:\n"
<< "rotation_matrix = \n"
<< rotation_matrix;
return rotation_matrix;
}
/**
* @brief Quaternion2AngleAxis 四元数 -> 轴角
* @param Quaternion(x-i, y-j, z-k, w) 前三个虚部,最后一个实部
* @retval Eigen::AngleAxisd
*/
Eigen::AngleAxisd Quaternion2AngleAxis(const double x, const double y,
const double z, const double w) {
Eigen::Quaterniond q(w, x, y, z); // 注意构造时第一个数字是w
Eigen::AngleAxisd angle_axis(q);
// 或者 使用=赋值,注意:一定要先构造,再赋值
Eigen::AngleAxisd angle_axis2;
angle_axis2 = q;
LOG(ERROR) << "Quaternion2AngleAxis result is:\n"
<< "rvec:axis:[" << angle_axis.axis().transpose()
<< "] ,angle(rad):" << angle_axis.angle();
return angle_axis;
}
/******************************************* 轴角 ************************/
/**
* @brief AngleAxis2RotationMatrix 轴角 -> 旋转矩阵
* @param Eigen::Matrix3d
* @retval Eigen:AngleAxisd
*/
Eigen::Matrix3d AngleAxis2RotationMatrix(Eigen::AngleAxisd angleaxisd) {
// 使用.toRotationMatrix()方法,罗德里格斯公式
Eigen::Matrix3d rotation_matrix = angleaxisd.toRotationMatrix();
// 或者使用.matrix()方法
Eigen::Matrix3d rotation_matrix2 = angleaxisd.matrix();
LOG(ERROR) << "AngleAxis2RotationMatrix result is:\n"
<< "rotation_matrix = \n"
<< rotation_matrix;
return rotation_matrix;
}
/**
* @brief AngleAxis2Euler 轴角 -> 欧拉角
* @param Eigen::AngleAxisd
* @retval Eigen:Vector3d Euler angle
* Euler sequence: z->y->x zyx ypr yaw,pitch,roll
* 注意:定义的Euler角顺序一定要一致
*/
Eigen::Vector3d AngleAxis2Euler(Eigen::AngleAxisd angleaxisd) {
Eigen::Vector3d euler = angleaxisd.matrix().eulerAngles(2, 1, 0);
LOG(ERROR) << "AngleAxis2Euler result is:\n"
<< "z,y,x|yaw,pitch,roll = [" << euler[0] << "," << euler[1] << ","
<< euler[2] << "]";
return euler;
}
/**
* @brief AngleAxis2Quaternion 轴角 -> 四元数
* @param Eigen::AngleAxisd
* @retval Eigen:Quaterniond
*/
Eigen::Quaterniond AngleAxis2Quaternion(Eigen::AngleAxisd angleaxisd) {
Eigen::Quaterniond q(angleaxisd);
// 或者 使用=赋值,注意:一定要先构造,再赋值
Eigen::Quaterniond q2;
q2 = angleaxisd;
LOG(ERROR) << "AngleAxis2Quaternion result is:\n"
<< "w,x,y,z = [" << q.w() << "," << q.x() << "," << q.y() << ","
<< q.z() << "]";
return q;
}
/******************************************* 旋转矩阵 ************************/
/**
* @brief RotationMatrix2Quaternion 旋转矩阵 -> 四元数
* @param Eigen::Matrix3d RotationMatrix
* @retval Quaterniond
*/
Eigen::Quaterniond RotationMatrix2Quaternion(Eigen::Matrix3d rotation_matrix) {
Eigen::Quaterniond q = Eigen::Quaterniond(rotation_matrix);
// 或者 使用=赋值,注意:一定要先构造,再赋值
Eigen::Quaterniond q2;
q2 = rotation_matrix;
q.normalize();
LOG(ERROR) << "RotationMatrix2Quaternion result is:\n"
<< "w,x,y,z = [" << q.w() << "," << q.x() << "," << q.y() << ","
<< q.z() << "]";
return q;
}
/**
* @brief RotationMatrix2Euler 旋转矩阵 -> 欧拉角
* @param Eigen::Matrix3d
* @retval Eigen::Vector3d euler_angle zyx ypr yaw,pitch,roll
*/
Eigen::Vector3d RotationMatrix2Euler(Eigen::Matrix3d rotation_matrix) {
Eigen::Vector3d euler =
rotation_matrix.eulerAngles(2, 1, 0); // zyx ypr yaw,pitch,roll
LOG(ERROR) << "RotationMatrix2Euler result is:\n"
<< "z,y,x|yaw,pitch,roll = [" << euler[0] << "," << euler[1] << ","
<< euler[2] << "]"
<< "\n"
// radian to angle
<< "[" << euler[0] * (180.0 / M_PI) << "deg, "
<< euler[1] * (180.0 / M_PI) << "deg, "
<< euler[2] * (180.0 / M_PI) << "deg]";
return euler;
}
/**
* @brief RotationMatrix2AngleAxis 旋转矩阵 -> 轴角
* @param Eigen::Matrix3d
* @retval Eigen:AngleAxisd
*/
Eigen::AngleAxisd RotationMatrix2AngleAxis(Eigen::Matrix3d rotation_matrix) {
Eigen::AngleAxisd angle_axis(rotation_matrix);
// 或者使用.fromRotationMatrix()方法
Eigen::AngleAxisd angle_axis2;
angle_axis2.fromRotationMatrix(rotation_matrix);
LOG(ERROR) << "RotationMatrix2AngleAxis result is:\n"
<< "rvec:axis:[" << angle_axis.axis().transpose()
<< "] ,angle(rad):" << angle_axis.angle();
return angle_axis;
}
} // namespace pose
4. 使用transforms3d的相互转换
注意与Eigen保持一致,euler_angle 为旋转轴欧拉角,顺序为zyx ypr yaw pitch roll
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
"""
Python Geometry using transforms3d
Python 几何库transforms3d使用笔记
- https://matthew-brett.github.io/transforms3d/index.html"""
# %%
import transforms3d as tfs
import numpy as np
""" notice: Euler sequence: z->y->x zyx ypr yaw,pitch,roll """
euler_test = [1.2, -1.4, 1.0] # yaw,pitch,roll
# %%
print("------------------------------------------------------")
# 欧拉角 -> 旋转矩阵
rotate_matrix = tfs.euler.euler2mat(euler_test[0], euler_test[1], euler_test[2],
"rzyx") # s 表示 固定轴欧拉角, r 表示 旋转轴欧拉角
print("rotate_matrix\n", rotate_matrix)
# 欧拉角 -> 轴角
vec, theta = tfs.euler.euler2axangle(euler_test[0], euler_test[1],
euler_test[2],
"rzyx")
print("angleaxis.v", vec)
print("angleaxis.theta", theta)
# 欧拉角 -> 四元数
quaternion = tfs.euler.euler2quat(euler_test[0], euler_test[1], euler_test[2],
"rzyx")
print("quaternion(w,x,y,z)", quaternion)
print("------------------------------------------------------")
# 四元数 -> 旋转矩阵
rotate_matrix = tfs.quaternions.quat2mat(quaternion)
print("rotate_matrx\n", rotate_matrix)
# 四元数 -> 轴角
vec, theta = tfs.quaternions.quat2axangle(quaternion)
print("angleaxis.v", vec)
print("angleaxis.theta", theta)
# 四元数 -> 欧拉角
euler_angle = tfs.euler.quat2euler(quaternion, 'rzyx')
print("euler_angle", euler_angle)
print("------------------------------------------------------")
# 轴角 -> 欧拉角
euler_angle = tfs.euler.axangle2euler(vec, theta, 'rzyx')
print("euler_angle", euler_angle)
# 轴角 -> 旋转矩阵
rotate_matrix = tfs.axangles.axangle2mat(vec, theta)
print("rotate_matrx\n", rotate_matrix)
# 轴角 -> 四元数
quaternion = tfs.quaternions.axangle2quat(vec, theta)
print("quaternion(w,x,y,z)", quaternion)
print("------------------------------------------------------")
# 旋转矩阵 -> 欧拉角
euler_angle = tfs.euler.mat2euler(rotate_matrix, "rzyx")
print("euler_angle", euler_angle)
# 旋转矩阵 -> 轴角
vec, theta = tfs.axangles.mat2axangle(rotate_matrix)
print("angleaxis.v", vec)
print("angleaxis.theta", theta)
# 或者
angleaxis = tfs.axangles.mat2axangle(rotate_matrix)
print("angleaxis", angleaxis)
print("angleaxis.v", angleaxis[0])
print("angleaxis.theta", angleaxis[1])
# 旋转矩阵 -> 四元数
quaternion = tfs.quaternions.mat2quat(rotate_matrix)
print("quaternion(w,x,y,z)", quaternion)
5. OpenCV中的位姿表达与转换
OpenCV提供了丰富的几何变换函数,主要在cv2模块中。
5.1 旋转向量(Rodrigues)与旋转矩阵
1
2
3
4
5
6
7
8
9
10
11
import cv2
import numpy as np
# 旋转向量 -> 旋转矩阵
rvec = np.array([0.1, 0.2, 0.3]) # 旋转向量 (轴角表示)
rotation_matrix, _ = cv2.Rodrigues(rvec)
print("Rotation Matrix:\n", rotation_matrix)
# 旋转矩阵 -> 旋转向量
rvec_back, _ = cv2.Rodrigues(rotation_matrix)
print("Rotation Vector:", rvec_back.flatten())
5.2 欧拉角与旋转矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import cv2
import numpy as np
def euler_to_rotation_matrix(yaw, pitch, roll):
"""欧拉角转旋转矩阵 (ZYX顺序)"""
# 分别计算绕各轴的旋转矩阵
R_z = np.array([[np.cos(yaw), -np.sin(yaw), 0],
[np.sin(yaw), np.cos(yaw), 0],
[0, 0, 1]])
R_y = np.array([[np.cos(pitch), 0, np.sin(pitch)],
[0, 1, 0],
[-np.sin(pitch), 0, np.cos(pitch)]])
R_x = np.array([[1, 0, 0],
[0, np.cos(roll), -np.sin(roll)],
[0, np.sin(roll), np.cos(roll)]])
# 组合旋转矩阵 (ZYX顺序)
R = R_z @ R_y @ R_x
return R
def rotation_matrix_to_euler(R):
"""旋转矩阵转欧拉角 (ZYX顺序)"""
sy = np.sqrt(R[0,0]**2 + R[1,0]**2)
singular = sy < 1e-6
if not singular:
x = np.arctan2(R[2,1], R[2,2]) # roll
y = np.arctan2(-R[2,0], sy) # pitch
z = np.arctan2(R[1,0], R[0,0]) # yaw
else:
x = np.arctan2(-R[1,2], R[1,1])
y = np.arctan2(-R[2,0], sy)
z = 0
return np.array([z, y, x]) # yaw, pitch, roll
5.3 PnP问题中的位姿估计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import cv2
import numpy as np
# 3D点和对应的2D投影点
object_points = np.array([[0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 1]], dtype=np.float32)
image_points = np.array([[100, 100], [200, 100], [100, 200], [150, 80]], dtype=np.float32)
# 相机内参
camera_matrix = np.array([[800, 0, 320], [0, 800, 240], [0, 0, 1]], dtype=np.float32)
dist_coeffs = np.zeros((4, 1))
# 求解PnP问题,得到旋转向量和平移向量
success, rvec, tvec = cv2.solvePnP(object_points, image_points, camera_matrix, dist_coeffs)
if success:
# 旋转向量转旋转矩阵
rotation_matrix, _ = cv2.Rodrigues(rvec)
print("Rotation Matrix:\n", rotation_matrix)
print("Translation Vector:", tvec.flatten())
6. PCL中的位姿表达与转换
PCL (Point Cloud Library) 提供了丰富的3D几何变换功能,主要在pcl::common模块中。
6.1 基本头文件
1
2
3
4
#include <pcl/common/transforms.h>
#include <pcl/common/eigen.h>
#include <pcl/common/angles.h>
#include <Eigen/Geometry>
6.2 变换矩阵操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <pcl/common/transforms.h>
#include <pcl/point_cloud.h>
#include <pcl/point_types.h>
#include <Eigen/Geometry>
// 创建变换矩阵
Eigen::Affine3f transform = Eigen::Affine3f::Identity();
// 设置平移
transform.translation() << 2.5, 0.0, 0.0;
// 设置旋转 (绕Z轴旋转45度)
transform.rotate(Eigen::AngleAxisf(M_PI/4, Eigen::Vector3f::UnitZ()));
// 应用变换到点云
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
pcl::PointCloud<pcl::PointXYZ>::Ptr transformed_cloud(new pcl::PointCloud<pcl::PointXYZ>);
pcl::transformPointCloud(*cloud, *transformed_cloud, transform);
6.3 欧拉角与变换矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <pcl/common/angles.h>
// 欧拉角转变换矩阵
float roll = pcl::deg2rad(30.0f); // 绕X轴旋转30度
float pitch = pcl::deg2rad(45.0f); // 绕Y轴旋转45度
float yaw = pcl::deg2rad(60.0f); // 绕Z轴旋转60度
Eigen::Affine3f transform = pcl::getTransformation(0, 0, 0, roll, pitch, yaw);
// 提取旋转矩阵
Eigen::Matrix3f rotation_matrix = transform.rotation();
// 提取平移向量
Eigen::Vector3f translation = transform.translation();
6.4 四元数操作
1
2
3
4
5
6
7
8
9
// 四元数转变换矩阵
Eigen::Quaternionf q(0.707, 0, 0, 0.707); // w, x, y, z
Eigen::Affine3f transform = Eigen::Affine3f::Identity();
transform.rotate(q);
// 变换矩阵转四元数
Eigen::Quaternionf quaternion(transform.rotation());
std::cout << "Quaternion (w,x,y,z): " << quaternion.w() << ", "
<< quaternion.x() << ", " << quaternion.y() << ", " << quaternion.z() << std::endl;
6.5 点云配准中的位姿估计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <pcl/registration/icp.h>
// ICP配准获得变换矩阵
pcl::IterativeClosestPoint<pcl::PointXYZ, pcl::PointXYZ> icp;
icp.setInputSource(source_cloud);
icp.setInputTarget(target_cloud);
pcl::PointCloud<pcl::PointXYZ> Final;
icp.align(Final);
if (icp.hasConverged()) {
// 获得变换矩阵
Eigen::Matrix4f transformation = icp.getFinalTransformation();
// 提取旋转和平移
Eigen::Matrix3f rotation = transformation.block<3,3>(0,0);
Eigen::Vector3f translation = transformation.block<3,1>(0,3);
std::cout << "Transformation matrix:\n" << transformation << std::endl;
}
7. 转换公式
- refitem:
欧拉角转四元数

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
struct Quaternion
{
double w, x, y, z;
};
Quaternion ToQuaternion(double yaw, double pitch, double roll) // yaw (Z), pitch (Y), roll (X)
{
// Abbreviations for the various angular functions
double cy = cos(yaw * 0.5);
double sy = sin(yaw * 0.5);
double cp = cos(pitch * 0.5);
double sp = sin(pitch * 0.5);
double cr = cos(roll * 0.5);
double sr = sin(roll * 0.5);
Quaternion q;
q.w = cy * cp * cr + sy * sp * sr;
q.x = cy * cp * sr - sy * sp * cr;
q.y = sy * cp * sr + cy * sp * cr;
q.z = sy * cp * cr - cy * sp * sr;
return q;
}
四元数转欧拉角

- arctan和arcsin的结果是
\([-\frac{\pi}{2},\frac{\pi}{2}]\)(https://private.codecogs.com/gif.latex?%5B-%5Cfrac%7B%5Cpi%7D%7B2%7D%2C%5Cfrac%7B%5Cpi%7D%7B2%7D%5D),这并不能覆盖所有朝向(对于
角\([\frac{\pi}{2},\frac{\pi}{2}]\)(https://private.codecogs.com/gif.latex?%5B-%5Cfrac%7B%5Cpi%7D%7B2%7D%2C%5Cfrac%7B%5Cpi%7D%7B2%7D%5D)的取值范围已经满足),因此需要用atan2来代替arctan。
- 符号约定 q0q1q2q3 qwqxqyqz
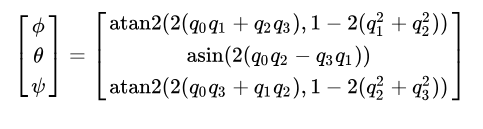
- 以上公式有一些奇异角未处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#define _USE_MATH_DEFINES
#include <cmath>
struct Quaternion {
double w, x, y, z; // q0,q1,q2,q3
};
struct EulerAngles {
double roll, pitch, yaw;
};
EulerAngles ToEulerAngles(Quaternion q) {
EulerAngles angles;
// yaw (z-axis rotation)
double siny_cosp = 2 * (q.w * q.z + q.x * q.y);
double cosy_cosp = 1 - 2 * (q.y * q.y + q.z * q.z);
angles.yaw = std::atan2(siny_cosp, cosy_cosp);
// pitch (y-axis rotation)
double sinp = 2 * (q.w * q.y - q.z * q.x);
if (std::abs(sinp) >= 1)
angles.pitch = std::copysign(M_PI / 2, sinp); // use 90 degrees if out of range
else
angles.pitch = std::asin(sinp);
// roll (x-axis rotation)
double sinr_cosp = 2 * (q.w * q.x + q.y * q.z);
double cosr_cosp = 1 - 2 * (q.x * q.x + q.y * q.y);
angles.roll = std::atan2(sinr_cosp, cosr_cosp);
return angles;
}
含有奇异角处理的转换
refitem:
- https://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToEuler/
singularities
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
* @brief quaternion to euler conversion
* @param quaternion qxqyqzqw
* @return euler yaw_angle, pitch_angle, roll_angle
* refitem:https://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToEuler/
*/
inline Eigen::Vector3f Quaterniond2Euler(const float qx, const float qy,
const float qz, const float qw) {
float yaw_angle, pitch_angle, roll_angle;
const float Threshold = 0.5f - Epsilon;
const float TEST = qw * qy - qz * qx;
if (TEST < -Threshold || TEST > Threshold) {
// singularities, pitch = ±90°
int sign = (TEST > 0) ? 1 : ((TEST < 0) ? -1 : 0);
yaw_angle = -2.0 * sign * (float)std::atan2(qx, qw);
pitch_angle = sign * (M_PI / 2.0);
roll_angle = 0.0;
} else {
yaw_angle = std::atan2(2.0 * (qw * qz + qx * qy),
qw * qw + qx * qx - qy * qy - qz * qz);
pitch_angle = std::asin(2 * (qw * qy - qz * qx));
roll_angle = std::atan2(2 * (qw * qx + qy * qz),
qw * qw - qx * qx - qy * qy + qz * qz);
}
Eigen::Vector3f euler(yaw_angle, pitch_angle, roll_angle);
return euler;
}
奇异范围的推算
1
2
3
4
5
pitch = math.asin(2 * (0.5 - epsilon)) * 180/ math.pi
epsilon = 0.5 - math.sin(pitch * math.pi / 180) / 2
threshold = 0.5 - epsilon
# 例如:需要pitch = 85degree时,可由第二行算出epsilon = 0.0019026
四元数转换旋转矩阵
- 符号约定 q0q1q2q3 qwqxqyqz
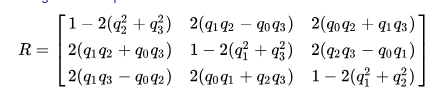
或等效地,通过齐次表达式:
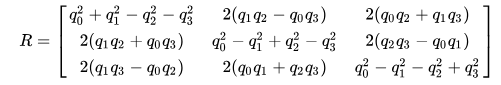
旋转矩阵转四元数
旋转矩阵转四元数有多种算法,这里提供Shepperd方法,该方法数值稳定性较好。
数学公式:
对于旋转矩阵 R:
1
2
3
R = [r11 r12 r13]
[r21 r22 r23]
[r31 r32 r33]
四元数 q = (w, x, y, z) 的计算公式:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
trace = r11 + r22 + r33
if trace > 0:
s = sqrt(trace + 1.0) * 2 // s = 4 * qw
qw = 0.25 * s
qx = (r32 - r23) / s
qy = (r13 - r31) / s
qz = (r21 - r12) / s
else if r11 > r22 && r11 > r33:
s = sqrt(1.0 + r11 - r22 - r33) * 2 // s = 4 * qx
qw = (r32 - r23) / s
qx = 0.25 * s
qy = (r12 + r21) / s
qz = (r13 + r31) / s
else if r22 > r33:
s = sqrt(1.0 + r22 - r11 - r33) * 2 // s = 4 * qy
qw = (r13 - r31) / s
qx = (r12 + r21) / s
qy = 0.25 * s
qz = (r23 + r32) / s
else:
s = sqrt(1.0 + r33 - r11 - r22) * 2 // s = 4 * qz
qw = (r21 - r12) / s
qx = (r13 + r31) / s
qy = (r23 + r32) / s
qz = 0.25 * s
C++实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <cmath>
struct Quaternion {
double w, x, y, z;
};
Quaternion RotationMatrixToQuaternion(const double R[3][3]) {
Quaternion q;
double trace = R[0][0] + R[1][1] + R[2][2];
if (trace > 0.0) {
double s = sqrt(trace + 1.0) * 2; // s = 4 * qw
q.w = 0.25 * s;
q.x = (R[2][1] - R[1][2]) / s;
q.y = (R[0][2] - R[2][0]) / s;
q.z = (R[1][0] - R[0][1]) / s;
} else if (R[0][0] > R[1][1] && R[0][0] > R[2][2]) {
double s = sqrt(1.0 + R[0][0] - R[1][1] - R[2][2]) * 2; // s = 4 * qx
q.w = (R[2][1] - R[1][2]) / s;
q.x = 0.25 * s;
q.y = (R[0][1] + R[1][0]) / s;
q.z = (R[0][2] + R[2][0]) / s;
} else if (R[1][1] > R[2][2]) {
double s = sqrt(1.0 + R[1][1] - R[0][0] - R[2][2]) * 2; // s = 4 * qy
q.w = (R[0][2] - R[2][0]) / s;
q.x = (R[0][1] + R[1][0]) / s;
q.y = 0.25 * s;
q.z = (R[1][2] + R[2][1]) / s;
} else {
double s = sqrt(1.0 + R[2][2] - R[0][0] - R[1][1]) * 2; // s = 4 * qz
q.w = (R[1][0] - R[0][1]) / s;
q.x = (R[0][2] + R[2][0]) / s;
q.y = (R[1][2] + R[2][1]) / s;
q.z = 0.25 * s;
}
return q;
}
// 使用Eigen的版本
Eigen::Quaterniond RotationMatrixToQuaternion(const Eigen::Matrix3d& R) {
Eigen::Quaterniond q;
double trace = R.trace();
if (trace > 0.0) {
double s = sqrt(trace + 1.0) * 2; // s = 4 * qw
q.w() = 0.25 * s;
q.x() = (R(2,1) - R(1,2)) / s;
q.y() = (R(0,2) - R(2,0)) / s;
q.z() = (R(1,0) - R(0,1)) / s;
} else if (R(0,0) > R(1,1) && R(0,0) > R(2,2)) {
double s = sqrt(1.0 + R(0,0) - R(1,1) - R(2,2)) * 2; // s = 4 * qx
q.w() = (R(2,1) - R(1,2)) / s;
q.x() = 0.25 * s;
q.y() = (R(0,1) + R(1,0)) / s;
q.z() = (R(0,2) + R(2,0)) / s;
} else if (R(1,1) > R(2,2)) {
double s = sqrt(1.0 + R(1,1) - R(0,0) - R(2,2)) * 2; // s = 4 * qy
q.w() = (R(0,2) - R(2,0)) / s;
q.x() = (R(0,1) + R(1,0)) / s;
q.y() = 0.25 * s;
q.z() = (R(1,2) + R(2,1)) / s;
} else {
double s = sqrt(1.0 + R(2,2) - R(0,0) - R(1,1)) * 2; // s = 4 * qz
q.w() = (R(1,0) - R(0,1)) / s;
q.x() = (R(0,2) + R(2,0)) / s;
q.y() = (R(1,2) + R(2,1)) / s;
q.z() = 0.25 * s;
}
return q.normalized();
}
Python实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
def rotation_matrix_to_quaternion(R):
"""
旋转矩阵转四元数 (Shepperd方法)
输入: 3x3旋转矩阵
输出: 四元数 [w, x, y, z]
"""
trace = np.trace(R)
if trace > 0:
s = np.sqrt(trace + 1.0) * 2 # s = 4 * qw
qw = 0.25 * s
qx = (R[2, 1] - R[1, 2]) / s
qy = (R[0, 2] - R[2, 0]) / s
qz = (R[1, 0] - R[0, 1]) / s
elif R[0, 0] > R[1, 1] and R[0, 0] > R[2, 2]:
s = np.sqrt(1.0 + R[0, 0] - R[1, 1] - R[2, 2]) * 2 # s = 4 * qx
qw = (R[2, 1] - R[1, 2]) / s
qx = 0.25 * s
qy = (R[0, 1] + R[1, 0]) / s
qz = (R[0, 2] + R[2, 0]) / s
elif R[1, 1] > R[2, 2]:
s = np.sqrt(1.0 + R[1, 1] - R[0, 0] - R[2, 2]) * 2 # s = 4 * qy
qw = (R[0, 2] - R[2, 0]) / s
qx = (R[0, 1] + R[1, 0]) / s
qy = 0.25 * s
qz = (R[1, 2] + R[2, 1]) / s
else:
s = np.sqrt(1.0 + R[2, 2] - R[0, 0] - R[1, 1]) * 2 # s = 4 * qz
qw = (R[1, 0] - R[0, 1]) / s
qx = (R[0, 2] + R[2, 0]) / s
qy = (R[1, 2] + R[2, 1]) / s
qz = 0.25 * s
# 归一化
norm = np.sqrt(qw*qw + qx*qx + qy*qy + qz*qz)
return np.array([qw/norm, qx/norm, qy/norm, qz/norm])
旋转矩阵 欧拉角
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import numpy as np
import math
def CheckRotationMatrix(R):
Rt = np.transpose(R)
shouldBeIdentity = np.dot(Rt, R)
I = np.identity(3, dtype=R.dtype)
n = np.linalg.norm(I - shouldBeIdentity)
return n < 1e-6
def RotationMatrixToEulerAngles(R):
assert (CheckRotationMatrix(R))
sy = math.sqrt(R[0,0]**2 + R[1,0]**2)
singular = sy < 1e-6
if not singular:
x = math.atan2(R[2,1], R[2,2]) # roll
y = math.atan2(-R[2,0], sy) # pitch
z = math.atan2(R[1,0], R[0,0]) # yaw
else:
x = math.atan2(-R[1,2], R[1,1])
y = math.atan2(-R[2,0], sy)
z = 0
return np.array([x, y, z])
def EulerAnglesToRotationMatrix(theta):
R_x = np.array([[1, 0, 0], [0, math.cos(theta[0]), -math.sin(theta[0])],
[0, math.sin(theta[0]),
math.cos(theta[0])]])
R_y = np.array([[math.cos(theta[1]), 0,
math.sin(theta[1])], [0, 1, 0],
[-math.sin(theta[1]), 0,
math.cos(theta[1])]])
R_z = np.array([[math.cos(theta[2]), -math.sin(theta[2]), 0],
[math.sin(theta[2]),
math.cos(theta[2]), 0], [0, 0, 1]])
R = np.dot(R_z, np.dot(R_y, R_x))
return R
Contact
Feel free to contact me windmillyucong@163.com anytime for anything.
