Ceres 优化库
- Ceres Solver
Created 2021.12.24 by William Yu; Last modified: 2022.08.11-V1.2.4
Contact: windmillyucong@163.com
Copyleft! 2022 William Yu. Some rights reserved.
Ceres Solver
References
- Tutorial http://ceres-solver.org/tutorial.html
- code https://github.com/ceres-solver/ceres-solver.git
- blog https://blog.csdn.net/liminlu0314/article/details/16808239
Install
Install ceres
1
2
3
4
5
6
7
8
9
10
sudo apt-get install liblapack-dev libsuitesparse-dev libcxsparse3.1.4 libgflags-dev libgoogle-glog-dev libgtest-dev
cd ~/src
git clone https://github.com/ceres-solver/ceres-solver.git
cd ceres-solver
mkdir build
cd build
cmake ..
make -j4
sudo make install
use ceres in CMake
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
################## add_third_party()
#
# CMake function to define a named third party library interface, with included
# headers and linked libraries.
#
# Parameters:
# NAME: name of target
# INCLUDES: list of include directories for the library
# LINKS: list of other libraries to be linked in to the library
# DEFINES: list of compile definitions
# COMPILE_OPTIONS: list of compile options
#
# Examples:
# add_third_party(
# NAME
# foo
# INCLUDES
# "${CMAKE_INSTALL_INCLUDEDIR}/foo"
# LINKS
# another
# DEFINES
# -Dbar
# COMPILE_OPTIONS
# -Wall
# )
function(ADD_THIRD_PARTY)
cmake_parse_arguments(ADD_THIRD_PARTY
""
"NAME"
"INCLUDES;LINKS;DEFINES;COMPILE_OPTIONS"
${ARGN})
unset(${ADD_THIRD_PARTY_NAME}_LIB_DEPENDS CACHE)
add_library(${ADD_THIRD_PARTY_NAME} INTERFACE)
target_include_directories(${ADD_THIRD_PARTY_NAME} INTERFACE
${ADD_THIRD_PARTY_INCLUDES})
target_link_libraries(${ADD_THIRD_PARTY_NAME} INTERFACE
${ADD_THIRD_PARTY_LINKS})
target_compile_definitions(${ADD_THIRD_PARTY_NAME} INTERFACE
${ADD_THIRD_PARTY_DEFINES})
target_compile_options(${ADD_THIRD_PARTY_NAME} INTERFACE
${ADD_THIRD_PARTY_COMPILE_OPTIONS})
endfunction(ADD_THIRD_PARTY)
## ceres_solver
find_package(Ceres REQUIRED)
if (Ceres_FOUND)
add_third_party(
NAME ceres_solver
INCLUDES ${CERES_INCLUDE_DIRS}
LINKS ${CERES_LIBRARIES}
)
else ()
message(STATUS "error:Ceres not found!!!!")
endif ()
- 注意点1:不要命名为ceres,会有重复命名,使用其他的比如ceres_lib, ceres_solver
- 注意点2:使用 CERES_LIBRARIES, 而不是CERES_LIBS
Demo
一个基本的使用Ceres 解决优化问题的例子
几个步骤:
- 定义cost function
- 创建 problem,并添加残差块
- 配置 solver
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 定义一个 cost function 结构体
struct CostFunctor {
// 重载() 传入待优化参数和残差
template <typename T>
bool operator()(const T* const x, T* residual) const {
residual[0] = T(10.0) - x[0];
return true;
}
};
int main(int argc, char** argv) {
google::InitGoogleLogging(argv[0]);
// The variable to solve for with its initial value.
const double initial_x = 5.0;
double x = initial_x;
// Build the problem.
Problem problem;
// Set up the only cost function (also known as residual). This uses
// auto-differentiation to obtain the derivative (jacobian).
// 参数:CostFunctor结构体,残差residual维度, 第一类待优化参数维度, 第二类待优化参数维度, ...
CostFunction* cost_function =
new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
// 参数依次是 cost_function loss_function, 第一类待优化参数, 第二类待优化参数, ...
problem.AddResidualBlock(cost_function, NULL, &x);
// Run the solver!
Solver::Options options;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
// 开始求解
Solver::Summary summary;
Solve(options, &problem, &summary);
// 输出log
std::cout << summary.BriefReport() << "\n";
std::cout << "x : " << initial_x << " -> " << x << "\n";
return 0;
}
注意:
两个地方需要传参
- CostFunctor的构造参数,传入会在()中使用到的常亮,该参数不会被优化
- 重载() 传入待优化参数和残差
Powell’s Function
Powell函数是一个常见的非线性优化测试函数,常用于评估优化算法的性能。其定义如下:
\[\begin{align} \\& f_1(x) = x_1 + 10 x_2 \\& f_2(x) = \sqrt 5 (x_3 - x_4) \\& f_3(x) = (x_2 - 2x_3)^2 \\& f_4(x) = \sqrt 10 (x_1 - x_4)^2 \end{align}\]其中 $x = [x_1, x_2, x_3, x_4]$ 是待优化的参数向量。
定义向量 G
\[G(x) = [f_1(x),f_2(x),f_3(x),f_4(x)]\]求解使得向量G的二范数最小的x
\[\underset x {\textrm {argmin}} F(x) = \underset x {\textrm {argmin}} \|G(x)\|^2 = \underset x {\textrm {argmin}} \sum_{i=1}^4 f_i(x) ^ 2\]每一个$f_i(x)$都是一个残差块
Powell函数最小值求解的Ceres实现
求解步骤如下:
- 定义CostFunctor
每一项都可以作为一个残差项,分别实现为不同的CostFunctor。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
struct F1 {
template <typename T>
bool operator()(const T* const x1, const T* const x2, T* residual) const {
residual[0] = x1[0] + 10.0 * x2[0];
return true;
}
};
struct F2 {
template <typename T>
bool operator()(const T* const x3, const T* const x4, T* residual) const {
residual[0] = sqrt(5.0) * (x3[0] - x4[0]);
return true;
}
};
struct F3 {
template <typename T>
bool operator()(const T* const x2, const T* const x3, T* residual) const {
residual[0] = (x2[0] - 2.0 * x3[0]) * (x2[0] - 2.0 * x3[0]);
return true;
}
};
struct F4 {
template <typename T>
bool operator()(const T* const x1, const T* const x4, T* residual) const {
residual[0] = sqrt(10.0) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
return true;
}
};
- 构建Problem并添加残差块
1
2
3
4
5
6
7
8
9
10
11
double x1 = 3.0, x2 = -1.0, x3 = 0.0, x4 = 1.0;
ceres::Problem problem;
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<F1, 1, 1, 1>(new F1), nullptr, &x1, &x2);
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<F2, 1, 1, 1>(new F2), nullptr, &x3, &x4);
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<F3, 1, 1, 1>(new F3), nullptr, &x2, &x3);
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<F4, 1, 1, 1>(new F4), nullptr, &x1, &x4);
- 配置求解器并求解
1
2
3
4
5
6
7
8
9
10
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
std::cout << summary.BriefReport() << std::endl;
std::cout << "x1 = " << x1 << ", x2 = " << x2
<< ", x3 = " << x3 << ", x4 = " << x4 << std::endl;
说明
- Powell函数的最优解为 $x_1 = 0, x_2 = 0, x_3 = 0, x_4 = 0$。
- 该例子展示了如何将复杂的目标函数拆分为多个残差块,每个残差块只依赖于部分参数。
- 通过这种方式,Ceres可以高效地处理大规模稀疏优化问题。
Curve Fitting
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
struct CurveFittingCost {
CurveFittingCost(double x, double y) : x_(x), y_(y) {}
/**
* @param[in] abc: 模型参数,是3维的
* @param[out] residual: 残差,1维
*/
template <typename T>
bool operator()(const T* const abc, T* residual) const {
/* error = y - exp(a*x^2 + b*x + c) */
residual[0] =
T(y_) - ceres::exp(abc[0] * T(x_) * T(x_) + abc[1] * T(x_) + abc[2]);
return true;
}
private:
const double x_, y_;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/// abc参数的初始估计值
double abc_hat[3] = {0, 0, 0};
/// 构建最小二乘问题
ceres::Problem problem;
for (int i = 0; i < samples_num; i++) {
// 添加误差项,参数:使用自动求导,模板参数:误差函数,残差维度,待估计参数维度
auto cost_func = new ceres::AutoDiffCostFunction<CurveFittingCost, 1, 3>(
new CurveFittingCost(x_sample[i], y_sample[i]));
// 向问题中添加误差项,参数:误差函数,核函数(nullptr 表示为空),待估计参数
problem.AddResidualBlock(cost_func, nullptr, abc_hat);
}
/// 配置求解器
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
BA
- 代码仓库:https://github.com/YuYuCong/sync/tree/develop/c%2B%2B/27.Ceres
- refitem:https://ceres-solver.googlesource.com/ceres-solver/+/master/examples/simple_bundle_adjuster.cc
0. BAL 数据集
数据集格式为:
1
2
3
4
5
6
7
8
9
10
11
12
13
/*
* 数据集格式:
* 第一行 相机数 点数 观测结果数
* 其余行 相机角标 点角标 观测结果
* 最后是 参数,即待优化项的初始值
* 参数每行一个
* 前面是相机参数,每9个一组,为一个相机的参数
* 相机的姿态
* 相机的位置
* 相机的内参
* 后面是点的参数,每3个一组,为一个点的参数
* 点的xyz坐标
*/
1. 重投影误差
具体公式详见2022-01-01-BA 以及 1.1 针孔相机的投影模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// Templated pinhole camera model for used with Ceres. The camera is
// parameterized using 9 parameters: 3 for rotation, 3 for translation, 1 for
// focal length and 2 for radial distortion. The principal point is not modeled
// (i.e. it is assumed be located at the image center).
// 重投影误差
struct SnavelyReprojectionError {
// 传入约束数值,常量,不会被优化
SnavelyReprojectionError(double observed_x, double observed_y)
: observed_x(observed_x), observed_y(observed_y) {}
// 传入被优化的参数和残差
template <typename T>
bool operator()(const T* const camera, const T* const point,
T* residuals) const {
// camera[0,1,2] are the angle-axis rotation.
T p[3];
ceres::AngleAxisRotatePoint(camera, point, p);
// camera[3,4,5] are the translation.
p[0] += camera[3];
p[1] += camera[4];
p[2] += camera[5];
// Compute the center of distortion. The sign change comes from
// the camera model that Noah Snavely's Bundler assumes, whereby
// the camera coordinate system has a negative z axis.
T xp = -p[0] / p[2];
T yp = -p[1] / p[2];
// Apply second and fourth order radial distortion.
const T& l1 = camera[7];
const T& l2 = camera[8];
T r2 = xp * xp + yp * yp;
T distortion = 1.0 + r2 * (l1 + l2 * r2);
// Compute final projected point position.
const T& focal = camera[6];
T predicted_x = focal * distortion * xp;
T predicted_y = focal * distortion * yp;
// The error is the difference between the predicted and observed position.
residuals[0] = predicted_x - observed_x;
residuals[1] = predicted_y - observed_y;
return true;
}
// Factory to hide the construction of the CostFunction object from
// the client code.
static ceres::CostFunction* Create(const double observed_x,
const double observed_y) {
// 残差的维度2,相机参数维度9,点参数维度3
return (new ceres::AutoDiffCostFunction<SnavelyReprojectionError, 2, 9, 3>(
new SnavelyReprojectionError(observed_x, observed_y)));
}
double observed_x;
double observed_y;
};
装填bal_problem,每个残差块需要三部分内容:输入观测计算出误差,该观测对应的相机参数,该观测对应的三维点世界坐标参数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
const double* observations = bal_problem.observations();
// Create residuals for each observation in the bundle adjustment problem. The
// parameters for cameras and points are added automatically.
ceres::Problem problem;
for (int i = 0; i < bal_problem.num_observations(); ++i) {
// Each Residual block takes a point and a camera as input and outputs a 2
// dimensional residual. Internally, the cost function stores the observed
// image location and compares the reprojection against the observation.
ceres::CostFunction* cost_function = SnavelyReprojectionError::Create(
observations[2 * i + 0], observations[2 * i + 1]);
problem.AddResidualBlock(cost_function, nullptr /* squared loss */,
bal_problem.mutable_camera_for_observation(i),
bal_problem.mutable_point_for_observation(i));
}
// Make Ceres automatically detect the bundle structure. Note that the
// standard solver, SPARSE_NORMAL_CHOLESKY, also works fine but it is slower
// for standard bundle adjustment problems.
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_SCHUR;
options.minimizer_progress_to_stdout = true;
tips
一个小注意,究竟ceres::AutoDiffCostFunction<SnavelyReprojectionError, 2, 9, 3>里面的数字怎么填写呢?去看用户定义的cost function里面重载的()的传入参数,最后一个传入参数residuals的维度就是第一个数字,然后再填入第一个参数的维度,第二个参数的维度…
pose_graph
代码仓库:https://github.com/YuYuCong/sync/tree/develop/c%2B%2B/27.Ceres
1. g2o文件详解
g2o数据集下载地址 https://lucacarlone.mit.edu/datasets/
g2o文件描述了一个位姿图问题,他由两部分组成:vertices 和 constraints。具体的文件格式如下:
2d
1
2
VERTEX_SE2 ID x_meters y_meters yaw_radians
EDGE_SE2 ID_A ID_B A_x_B A_y_B A_yaw_B I_11 I_12 I_13 I_22 I_23 I_33
3d
1
2
VERTEX_SE3:QUAT ID x y z q_x q_y q_z q_w
EDGE_SE3:QUAT ID_a ID_b x_ab y_ab z_ab q_x_ab q_y_ab q_z_ab q_w_ab I_11 I_12 I_13 ... I_16 I_22 I_23 ... I_26 ... I_66 // NOLINT
信息矩阵
其中 I_ij 是 (i, j)-th 观测的信息矩阵(information matrix),只存储上三角部分,测量顺序是 delta position,然后是 delta orientation.
- 每条边具有一个信息矩阵
- 用于度量不确定性
- 信息矩阵 Ω 是协方差矩阵的逆,是一个对称矩阵, 所以只用存储上三角部分
- 它的每个元素可以看成我们对ei,ej这个误差项相关性的一个预计
- 最简单的是把Ω设成对角矩阵,对角阵元素的大小表明我们对此项误差的重视程度
- 例如:你觉得帧间匹配精度在0.1m,那么把信息矩阵设成100的对角阵即可。 因为pose为6D的,信息矩阵是6*6的矩阵。
- 假设位置和角度的估计精度均为0.1且互相独立,那么协方差则为对角为0.01的矩阵,信息阵则为数值是100的矩阵。
- 当然也可以将角度设大一些,表示对角度的估计更加准确
1
2
3
4
Eigen::Matrix<double, 6, 6> information = Eigen::Matrix< double, 6,6 >::Identity();
information(0,0) = information(1,1) = information(2,2) = 100;
information(3,3) = information(4,4) = information(5,5) = 100;
edge->setInformation( information );
2. 残差推导
Refitem:
- Giorgio Grisetti, Rainer Kummerle, Cyrill Stachniss, Wolfram Burgard. A Tutorial on Graph-Based SLAM. IEEE Intelligent Transportation Systems Magazine, 52(3):199-222, 2010.
2d位姿残差
t时刻机器人的状态定义为 $x_t = [p^T, \xi]^T$ ,其中p表示2维平面位置(单位m),$\xi$ 表示方向(单位rad)。机器人在a,b 两个时刻的观测约束为a,b两个时刻的相对位姿变换,定义为$z_{ab}=[\hat p_{ab}^T,\hat\xi_{ab}]$。在Ceres中定义的残差即定义为测量值与观测值之间的差: \(r_{ab} = \begin{bmatrix} R_{a} ^T(p_b -p_a) - \hat p_{ab} \\ \text{Normalize} (\xi_a - \xi_b - \xi_{ab} ) \end{bmatrix}\)
其中 $\text{Normalize}$ 将角度归一化到$[-\pi,\pi)$ 范围内。其中$R_a$表示由姿态角度$\xi_a$定义的2维旋转矩阵。 \(R\{\theta\} \equiv \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\)
上面计算出的$r_{ab}$是个矩阵,不是个数值,无法用于误差计算,所以使用观测的协方差矩阵(covariance matrix)的逆方根来计算最终的具体误差数值
\[e_{ab} = \Sigma^{-\frac 1 2}_{ab} r_{ab}\]代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class PoseGraph2dErrorTerm {
public:
PoseGraph2dErrorTerm(double x_ab,
double y_ab,
double yaw_ab_radians,
const Eigen::Matrix3d& sqrt_information)
: p_ab_(x_ab, y_ab),
yaw_ab_radians_(yaw_ab_radians),
sqrt_information_(sqrt_information) {}
template <typename T>
bool operator()(const T* const x_a,
const T* const y_a,
const T* const yaw_a,
const T* const x_b,
const T* const y_b,
const T* const yaw_b,
T* residuals_ptr) const {
const Eigen::Matrix<T, 2, 1> p_a(*x_a, *y_a);
const Eigen::Matrix<T, 2, 1> p_b(*x_b, *y_b);
Eigen::Map<Eigen::Matrix<T, 3, 1>> residuals_map(residuals_ptr);
residuals_map.template head<2>() =
RotationMatrix2D(*yaw_a).transpose() * (p_b - p_a) - p_ab_.cast<T>();
residuals_map(2) = ceres::examples::NormalizeAngle(
(*yaw_b - *yaw_a) - static_cast<T>(yaw_ab_radians_));
// Scale the residuals by the square root information matrix to account for
// the measurement uncertainty. residuals_map = sqrt_information_.template cast<T>() * residuals_map;
return true; }
static ceres::CostFunction* Create(double x_ab,
double y_ab,
double yaw_ab_radians,
const Eigen::Matrix3d& sqrt_information) {
return (new ceres::
AutoDiffCostFunction<PoseGraph2dErrorTerm, 3, 1, 1, 1, 1, 1, 1>(
new PoseGraph2dErrorTerm(
x_ab, y_ab, yaw_ab_radians, sqrt_information)));
}
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
private:
// The position of B relative to A in the A frame.
const Eigen::Vector2d p_ab_;
// The orientation of frame B relative to frame A.
const double yaw_ab_radians_;
// The inverse square root of the measurement covariance matrix.
const Eigen::Matrix3d sqrt_information_;
};
3d位姿残差
同上,$x_t = [p^T, q]^T$ ,$p^T$ 为三维位置,$q$ 为四元数表达的三维姿态,残差项定义为
\[r_{ab} = \begin{bmatrix}R(q_a)^T(p_a - p_b) - \hat p_{ab}\\ 2.0\text{vec}((q_a^{-1}q_b)\hat q_{ab}^{-1}) \end{bmatrix}\]where the function $\text{vec}()$ returns the vector part of the quaternion, i.e. [qx,qy,qz], and $R(q)$ is the rotation matrix for the quaternion.
注意:
- 如果我们需要评价两个旋转矩阵$R_a$与$R_b$的相似程度,可以求$R_aR_b^T$,其与I 越接近,说明误差越小。
- 同理,如果需要评价两个四元数$q_a$ 与 $q_b$ 的相似程度,可以求$q_a q_b^{-1}$。
同样,我们需要给r乘上信息矩阵。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class PoseGraph3dErrorTerm {
public:
PoseGraph3dErrorTerm(const Pose3d& t_ab_measured,
const Eigen::Matrix<double, 6, 6>& sqrt_information)
: t_ab_measured_(t_ab_measured), sqrt_information_(sqrt_information) {}
template <typename T>
bool operator()(const T* const p_a_ptr,
const T* const q_a_ptr,
const T* const p_b_ptr,
const T* const q_b_ptr,
T* residuals_ptr) const {
Eigen::Map<const Eigen::Matrix<T, 3, 1>> p_a(p_a_ptr);
Eigen::Map<const Eigen::Quaternion<T>> q_a(q_a_ptr);
Eigen::Map<const Eigen::Matrix<T, 3, 1>> p_b(p_b_ptr);
Eigen::Map<const Eigen::Quaternion<T>> q_b(q_b_ptr);
// Compute the relative transformation between the two frames.
Eigen::Quaternion<T> q_a_inverse = q_a.conjugate();
Eigen::Quaternion<T> q_ab_estimated = q_a_inverse * q_b;
// Represent the displacement between the two frames in the A frame.
Eigen::Matrix<T, 3, 1> p_ab_estimated = q_a_inverse * (p_b - p_a);
// Compute the error between the two orientation estimates.
Eigen::Quaternion<T> delta_q =
t_ab_measured_.q.template cast<T>() * q_ab_estimated.conjugate();
// Compute the residuals.
// [ position ] [ delta_p ] // [ orientation (3x1)] = [ 2 * delta_q(0:2) ] Eigen::Map<Eigen::Matrix<T, 6, 1>> residuals(residuals_ptr);
residuals.template block<3, 1>(0, 0) =
p_ab_estimated - t_ab_measured_.p.template cast<T>();
residuals.template block<3, 1>(3, 0) = T(2.0) * delta_q.vec();
// Scale the residuals by the measurement uncertainty.
residuals.applyOnTheLeft(sqrt_information_.template cast<T>());
return true; }
static ceres::CostFunction* Create(
const Pose3d& t_ab_measured,
const Eigen::Matrix<double, 6, 6>& sqrt_information) {
return new ceres::AutoDiffCostFunction<PoseGraph3dErrorTerm, 6, 3, 4, 3, 4>(
new PoseGraph3dErrorTerm(t_ab_measured, sqrt_information));
}
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
private:
// The measurement for the position of B relative to A in the A frame.
const Pose3d t_ab_measured_;
// The square root of the measurement information matrix.
const Eigen::Matrix<double, 6, 6> sqrt_information_;
};
优化结果:
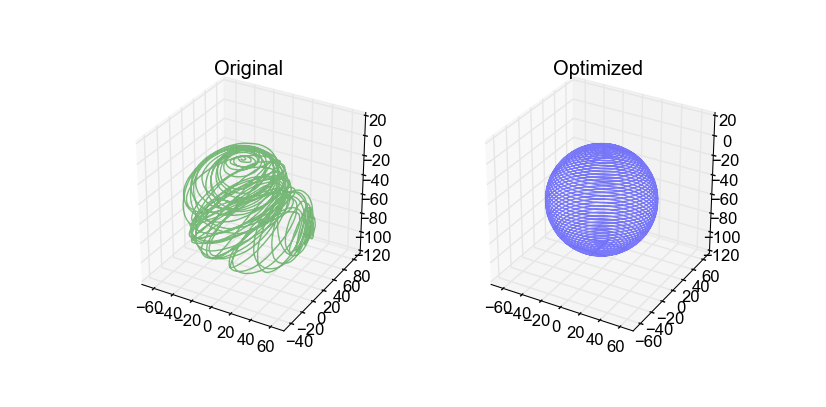
API 详解
Derivatives
微分
1. Automatic 自动微分
基于复合函数求导链式法则,获得导数的解析解
1
AutoDiffCostFunction
用户定义cost 结构体
1
2
3
4
5
6
7
8
struct CostFunctor {
template <typename T>
bool operator()(const T* const x, T* residual) const {
residual[0] = T(10.0) - x[0];
return true;
}
};
添加 AddResidualBlock
1
2
3
CostFunction* cost_function =
new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
problem.AddResidualBlock(cost_function, NULL, &x);
2. Numeric 数值微分
1
AutoDiffCostFunction
使用场景:
某些情况下,无法定义模板化的cost function。比如:当残差估计涉及到一些无法控制的库函数的调用,或者使用无法控制的外部函数的时候。这种情况下,需要使用数值微分。
1
2
3
4
5
6
struct NumericDiffCostFunctor {
bool operator()(const double* const x, double* residual) const {
residual[0] = 10.0 - x[0];
return true;
}
};
1
2
3
4
CostFunction* cost_function =
new NumericDiffCostFunction<NumericDiffCostFunctor, ceres::CENTRAL, 1, 1>(
new NumericDiffCostFunctor);
problem.AddResidualBlock(cost_function, nullptr, &x);
注意对比之前的自动微分
1
2
3
CostFunction* cost_function =
new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
problem.AddResidualBlock(cost_function, nullptr, &x);
细节:
-
数值微分的构造 new NumericDiffCostFunction
自动微分的构造 new AutoDiffCostFunction
-
数值微分的构造多了一个参数:
建议:
- 建议使用自动微分,而不是数值微分
- 使用c++模板类可以提高自动微分的效率
- 数值微分的成本比较高
- 数值微分容易出现数值错误,导致收敛速度变慢
3. Analytic 解析微分
使用场景:
- 用户需要自行提供导数的计算解析式
- 函数简单,可以自行推导出导数的解析式
- 性能有极致要求
某些情况下,无法使用自动微分。比如:For example, it may be the case that it is more efficient to compute the derivatives in closed form instead of relying on the chain rule used by the automatic differentiation code.
In such cases, it is possible to supply your own residual and jacobian computation code. To do this, define a subclass of CostFunction or SizedCostFunction if you know the sizes of the parameters and residuals(残差) at compile time.
在这种情况下,可以实现自己的 residual 和 jacobian 计算代码。
在编译的时候就知道 参数和parameters 和 residuals的大小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class QuadraticCostFunction : public ceres::SizedCostFunction<1, 1> {
public:
virtual ~QuadraticCostFunction() {}
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const {
const double x = parameters[0][0];
residuals[0] = 10 - x;
// Compute the Jacobian if asked for.
if (jacobians != nullptr && jacobians[0] != nullptr) {
jacobians[0][0] = -1;
}
return true;
}
};
Log
提供两种日志:
- 简报 BriefReport()
- 全报 FullReport()
1
2
3
4
5
6
7
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
// brief report
std::cout << summary.BriefReport() << std::endl;
// full log
std::cout << summary.FullReport() << std::endl;
Options
配置求解过程中的各项参数。
1
2
3
4
5
6
ceres::Solver::Options options;
options.max_num_iterations = 100; // 最大迭代次数
options.gradient_tolerance = 1e-16; // 迭代收敛条件
options.function_tolerance = 1e-16; // 迭代收敛条件
options.linear_solver_type = ceres::SPARSE_NORMAL_CHOLESKY; // 求解器的种类
options.num_linear_solver_threads = 4; // 求解线程
LinearSolverType
求解器的种类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
enum LinearSolverType {
// These solvers are for general rectangular systems formed from the
// normal equations A'A x = A'b. They are direct solvers and do not
// assume any special problem structure.
// Solve the normal equations using a dense Cholesky solver; based
// on Eigen.
DENSE_NORMAL_CHOLESKY,
// Solve the normal equations using a dense QR solver; based on
// Eigen.
DENSE_QR,
// Solve the normal equations using a sparse cholesky solver; requires
// SuiteSparse or CXSparse.
SPARSE_NORMAL_CHOLESKY,
// Specialized solvers, specific to problems with a generalized
// bi-partitite structure.
// Solves the reduced linear system using a dense Cholesky solver;
// based on Eigen.
DENSE_SCHUR,
// Solves the reduced linear system using a sparse Cholesky solver;
// based on CHOLMOD.
SPARSE_SCHUR,
// Solves the reduced linear system using Conjugate Gradients, based
// on a new Ceres implementation. Suitable for large scale
// problems.
ITERATIVE_SCHUR,
// Conjugate gradients on the normal equations.
CGNR
};
LossFunction
Loss核函数
1
2
3
4
5
6
7
8
9
10
TrivialLoss
HuberLoss
SoftLOneLoss
CauchyLoss
ArctanLoss
TolerantLoss
TukeyLoss
ComposedLoss
ScaledLoss
LossFunctionWrapper
AddResidualBlock
1
2
3
4
problem->AddResidualBlock(
cost_function, loss_function, &pose_begin_iter->second.x,
&pose_begin_iter->second.y, &pose_end_iter->second.x,
&pose_end_iter->second.y);
SetParameterBlockConstant
对于某些不希望被优化的量,可以使用SetParameterBlockConstant() 方法固定其参数
1
2
3
4
std::map<int, Point2d>::iterator pose_start_iter = poses->begin();
CHECK(pose_start_iter != poses->end()) << "There are no poses.";
problem->SetParameterBlockConstant(&pose_start_iter->second.x);
problem->SetParameterBlockConstant(&pose_start_iter->second.y);
原理
Ceres 内部实现的优化原理是什么呢?
参考:
Ceres Solver 是一个用于求解非线性最小二乘问题的开源C++库,它提供了多种优化算法:
- 信赖域方法:
- Levenberg-Marquardt(默认)
- Dogleg
- Subspace Dogleg
- 线搜索方法:
- Wolfe条件线搜索
- Armijo条件线搜索
- 预处理技术:
- Jacobi预处理
- Incomplete Cholesky预处理
- Schur补预处理(用于BA问题)
- 求解器选项:
- DENSE_QR:用于小规模问题
- DENSE_NORMAL_CHOLESKY:用于中等规模问题
- SPARSE_NORMAL_CHOLESKY:用于大规模稀疏问题
- CGNR:共轭梯度法
- ITERATIVE_SCHUR:用于BA问题
尝试自己实现一个优化库?
Contact
Feel free to contact me windmillyucong@163.com anytime for anything.
