Bundle Adjustment 光束平差，是同时优化相机的位姿与观测点的一类优化问题，是SLAM算法的核心部分。本文简单总结BA的原理与推导，以及求解过程。

• Bundle Adjustment
  • 0. Concepts
  • 1. BA 问题
  • 2. BA 问题求解
    • 2.1 增量方程
    • 2.2 梯度推导
      • 2.2.1 投影误差对相机坐标系下点的导数
      • 2.2.2 相机坐标系下点对相机位姿的导数
      • 2.2.3 相机坐标系下点对世界坐标点的导数
      • 2.2.4 完整的雅可比矩阵
    • 2.3 海森矩阵的稀疏性
      • 2.3.1 稀疏结构
      • 2.3.2 稀疏结构的具体表现
        • 1 H_cc 的稀疏性
        • 2 H_pp 的稀疏性
        • 2 H_cp 的稀疏性
      • 2.3.3 稀疏性的优势
        • 1 内存效率
        • 2 计算效率
      • 2.3.4 稀疏性的数学意义
      • 2.3.5 实际例子
    • 2.4 舒尔补求解
      • 2.4.1 舒尔补原理
      • 2.4.2 在BA中的应用
  • 3 代码实现
    • 3.1 Ceres求解器
    • 3.2 其他优化库
  • 4. Related Works
    • 4.1 Parallel BA
    • 4.2 Hierarchical BA
    • 4.3 Segment-based BA
    • 4.4 Incremental BA
  • Contact
  • License

Created 2022.01.01 by Cong Yu; Last modified: 2022.01.01-v1.0.2

Contact: windmillyucong@163.com

Copyleft! 2022 Cong Yu. Some rights reserved.

Bundle Adjustment

References

• Paper Bundle Adjustment — A Modern Synthesis

0. Concepts

默认读者已经知晓的概念：

• 观测方程 1.1 针孔相机的投影模型
• 相机位姿

• 三维空间点

• Bundle Adjustment 光束平差
• Non-linear Optimization 非线性优化

1. BA 问题

数据：多个相机$C_1,…,C_i,…,C_m$，多个三维空间点$p_1,…p_j,…,p_n$。

观测时相机的位姿存在误差，点的位置存在误差，观测过程也存在误差。这些误差导致位姿是无法精确求解的。所以，BA问题构建为最优化问题。

相机观测这些点，得到真实观测像素值$z_{ij}$；同时，可由理想观测方程：$h(\xi_i, p_j)$，输入相机位姿$\xi_i$，输入三维点位置$p_j$，得到理想观测像素值。

两者之间的误差$e$即我们要最小化的目标： \(e_{ij} =z_{ij} - h(\xi_i,p_j) \tag1\)

上式只考虑了一个相机对一个三维点的误差，考虑整个BA问题，共m个相机和n个三维点，最多产生$mn$ 个观测，我们要同时调整所有的相机的位姿和所有三维点的位置，最小化整体的误差，所以VSLAM系统中的问题表达为： \(\underset{(\mathbf{\xi, p}) } {\text{argmin}} \sum_{i=1}^{m} \sum_{j=1}^{n} \frac 1 2 \|z_{ij} - h(\xi_i,p_j)\|^2 \tag2\) ^bd48db

其中 $(\mathbf{\xi, p}) \equiv \begin{bmatrix} \xi_1,…,\xi_i,…,\xi_m,p_1,…,p_j,…p_n \end{bmatrix}^T$ 表示所有待优化的位姿与所有三维点。

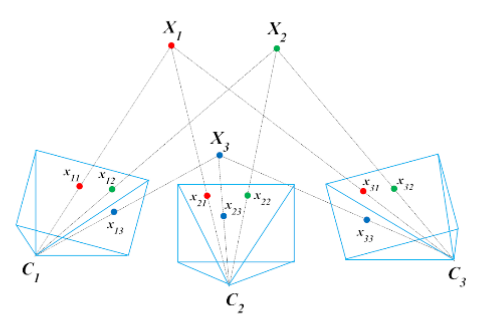
Fig1. ba

BA优化问题的求解过程：由于式(2) 的形式过于复杂，数值求解公式比较难以得出，可以使用优化方法求解。从某个初始值开始，对待优化参数$(\mathbf{\xi, p}) \equiv \begin{bmatrix} \xi_1,…,\xi_i,…,\xi_m,p_1,…,p_j,…p_n \end{bmatrix}^T$ 寻找梯度下降的方向，更新增量 $(\Delta\mathbf{\xi}, \Delta\mathbf{p})$，迭代优化即可。

2. BA 问题求解

2.1 增量方程

BA问题属于非线性最小二乘优化问题，其典型解法是高斯-牛顿法迭代方法，需要求解增量方程。数学推导详见 2022-01-04-最小二乘优化 中的 高斯牛顿法小节。

非线性最小二乘优化问题 的 增量方程： \(H_F \Delta x = -J_F^T\) 其中 \(\begin{align} &J_F = J_f^T f \\ &H_F \approx J_f^T J_f \end{align}\)

在BA中的应用：

• 此处的F即完整的BA优化目标函数 $\sum_{i=1}^{m} \sum_{j=1}^{n} \frac 1 2 |z_{ij} - h(\xi_i,p_j)|^2$
• 此处的f即上文的$e_{ij} =z_{ij} - h(\xi_i,p_j) \tag1$
• 求出 J_f，即可求出 J_F
• 求出 J_f，即可近似出 H_F
• 这种近似使得计算更加高效，保持了问题的稀疏结构，便于使用舒尔补进行求解

基于上述雅可比矩阵，我可以构建海森矩阵：

其中：

• $H_{cc}$ 是相机-相机块，大小为 $6m \times 6m$
• $H_{pp}$ 是点-点块，大小为 $3n \times 3n$
• $H_{cp}$ 是相机-点块，大小为 $6m \times 3n$

参数 $x$ 包含相机位姿 $\xi$ 和三维点 $p$ 两部分，因此最终的增量方程： \(\begin{bmatrix} H_{cc} & H_{cp} \\ H_{cp}^T & H_{pp} \end{bmatrix} \begin{bmatrix} \Delta \xi \\ \Delta p \end{bmatrix} = \begin{bmatrix} b_c \\ b_p \end{bmatrix}\)

• 其中 $b_c = -\sum_{i,j} J_{\xi_i}^T e_{ij}$ 和 $b_p = -\sum_{i,j} J_{p_j}^T e_{ij}$ 分别是相机和点对应的负雅可比矩阵乘以误差向量的累加

物理意义：

• $\Delta \xi$ 表示相机位姿的更新量
• $\Delta p$ 表示三维点的更新量
• 方程表示在当前参数下，如何调整相机位姿和三维点位置以最小化重投影误差

2.2 梯度推导

在BA问题中，我们涉及三个坐标系：

1. 世界坐标系（World Frame）：三维点 $p_j$ 的原始坐标
2. 相机坐标系（Camera Frame）：点 $p_j$ 在相机 $C_i$ 下的坐标，记为 $p_{ij}$
3. 图像坐标系（Image Frame）：投影后的像素坐标

其中 $p_{ij}$ 表示点 $p_j$ 在相机 $C_i$ 的坐标系下的坐标，通过相机位姿变换得到： \(p_{ij} = \mathbf{R}_i p_j + \mathbf{t}_i\)

对于式(2)中的误差项，我们可以将其展开为：

其中，$[X_{ij}, Y_{ij}, Z_{ij}]^T$ 是点 $p_j$ 在相机 $C_i$ 坐标系下的坐标。根据链式法则，误差对相机位姿和三维点的雅可比矩阵为：

让我们详细推导每一步：

2.2.1 投影误差对相机坐标系下点的导数

首先计算 $\frac{\partial e_{ij}}{\partial p_{ij}}$：

2.2.2 相机坐标系下点对相机位姿的导数

对于相机位姿 $\xi_i = [\mathbf{t}_i, \mathbf{R}_i]$，其中 $\mathbf{t}_i$ 是平移向量，$\mathbf{R}_i$ 是旋转矩阵（使用李代数表示）。点从世界坐标系到相机坐标系的变换为：

因此：

其中 $[\cdot]_\times$ 表示反对称矩阵。

对于向量 $\mathbf{a} = [a_1, a_2, a_3]^T$，其反对称矩阵为：

反对称矩阵在BA中的作用：

1. 用于表示旋转矩阵的李代数形式
2. 在计算雅可比矩阵时，用于表示旋转对点的导数
3. 具有性质：$[\mathbf{a}]_\times \mathbf{b} = \mathbf{a} \times \mathbf{b}$，其中 $\times$ 表示叉积

2.2.3 相机坐标系下点对世界坐标点的导数

对于世界坐标系下的点 $p_j$：

2.2.4 完整的雅可比矩阵

将上述结果组合，得到完整的雅可比矩阵：

误差对相机位姿的雅可比矩阵为：

误差对世界坐标下三维点的雅可比矩阵为：

2.3 海森矩阵的稀疏性

2.3.1 稀疏结构

海森矩阵的稀疏性主要来源于观测的稀疏性：

• 观测稀疏性：在SLAM中，并不是每个相机都能观测到每个三维点
• 参数独立性：不同相机之间、不同三维点之间在大多数情况下是相互独立的
• 局部连接：只有存在观测关系的相机-点对才会产生非零的雅可比矩阵块

2.3.2 稀疏结构的具体表现

1 H_cc 的稀疏性

相机-相机块通常具有块对角结构：

• 每个对角线块 $H_{ii}$ 表示第i个相机的自耦合（6×6矩阵）
• 非对角线块通常为零，因为不同相机位姿之间通常没有直接约束关系
• 只有在相机之间存在约束（如回环检测）时，非对角线块才非零

2 H_pp 的稀疏性

点-点块也具有块对角结构：

• 每个对角线块 $H_{ii}$ 表示第i个三维点的自耦合（3×3矩阵）
• 非对角线块通常为零，因为不同三维点之间通常没有直接约束关系
• 只有在点之间存在约束（如共面约束）时，非对角线块才非零

2 H_cp 的稀疏性

相机-点块反映了观测关系：

• 只有当相机i观测到点j时，$H_{ij}$ 才非零
• 大多数元素为零，因为观测是稀疏的
• 这种稀疏性反映了相机与三维点之间的观测拓扑结构

2.3.3 稀疏性的优势

1 内存效率

• 密集矩阵：需要存储 $(6m+3n)^2$ 个元素
• 稀疏矩阵：只需要存储非零块，大大减少内存使用
• 实际节省：对于大规模问题，内存节省可达90%以上

2 计算效率

• 舒尔补求解：利用稀疏结构将复杂度从 $O((6m+3n)^3)$ 降低到 $O(m^3 + n^3)$
• 并行计算：稀疏结构便于并行处理
• 数值稳定性：稀疏结构通常具有更好的条件数

2.3.4 稀疏性的数学意义

这种稀疏结构反映了BA问题的图结构：

• 节点：相机和三维点
• 边：观测关系
• 稀疏性：大多数节点之间没有直接连接

这种图结构使得我们可以使用图优化的方法来高效求解BA问题，这也是为什么现代SLAM系统能够处理大规模场景的关键原因之一。

这种稀疏结构使得我们可以使用舒尔补来高效求解增量方程。

2.3.5 实际例子

假设有3个相机和4个三维点，观测关系如下：

1
2
3
相机1观测点1,2
相机2观测点2,3  
相机3观测点3,4

对应的海森矩阵结构：

其中：

• 上半部分：相机-相机块（3×3）和相机-点块（3×4）
• 下半部分：点-相机块（4×3）和点-点块（4×4）
• 零块表示没有观测关系
• 非零块表示存在观测关系

2.4 舒尔补求解

2.4.1 舒尔补原理

对于分块矩阵： \(M = \begin{bmatrix} A & B \\ C & D \end{bmatrix}\)

其中 $A$ 是可逆矩阵，其逆矩阵可以表示为： \(M^{-1} = \begin{bmatrix} A^{-1} + A^{-1}BS^{-1}CA^{-1} & -A^{-1}BS^{-1} \\ -S^{-1}CA^{-1} & S^{-1} \end{bmatrix}\)

其中 $S = D - CA^{-1}B$ 是舒尔补。

推导过程：

设 $M^{-1} = \begin{bmatrix} X & Y \ Z & W \end{bmatrix}$，则： \(\begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} X & Y \\ Z & W \end{bmatrix} = \begin{bmatrix} I & 0 \\ 0 & I \end{bmatrix}\)

展开得到四个方程：

1. $AX + BZ = I$ → $X = A^{-1}(I - BZ)$
2. $AY + BW = 0$ → $Y = -A^{-1}BW$
3. $CX + DZ = 0$ → $CX + DZ = 0$
4. $CY + DW = I$ → $CY + DW = I$

将方程1代入方程3： \(C(A^{-1}(I - BZ)) + DZ = 0 \\ CA^{-1} - CA^{-1}BZ + DZ = 0 \\ (D - CA^{-1}B)Z = -CA^{-1} \\ SZ = -CA^{-1} \\ Z = -S^{-1}CA^{-1}\)

将方程2代入方程4： \(C(-A^{-1}BW) + DW = I \\ -CA^{-1}BW + DW = I \\ (D - CA^{-1}B)W = I \\ SW = I \\ W = S^{-1}\)

因此： \(X = A^{-1}(I - BZ) = A^{-1}(I + BS^{-1}CA^{-1}) = A^{-1} + A^{-1}BS^{-1}CA^{-1} \\ Y = -A^{-1}BW = -A^{-1}BS^{-1}\)

2.4.2 在BA中的应用

在BA问题中，我们有： \(H = \begin{bmatrix} H_{cc} & H_{cp} \\ H_{cp}^T & H_{pp} \end{bmatrix}\)

其逆矩阵为： \(H^{-1} = \begin{bmatrix} H_{cc}^{-1} + H_{cc}^{-1}H_{cp}S^{-1}H_{cp}^TH_{cc}^{-1} & -H_{cc}^{-1}H_{cp}S^{-1} \\ -S^{-1}H_{cp}^TH_{cc}^{-1} & S^{-1} \end{bmatrix}\)

其中 $S = H_{pp} - H_{cp}^TH_{cc}^{-1}H_{cp}$ 是舒尔补。

求解步骤：

• 首先求解相机增量： \((H_{cc} - H_{cp}H_{pp}^{-1}H_{cp}^T)\Delta \xi = b_c - H_{cp}H_{pp}^{-1}b_p\)
• 然后求解点增量： \(\Delta p = H_{pp}^{-1}(b_p - H_{cp}^T\Delta \xi)\)

3 代码实现

3.1 Ceres求解器

参考2021-12-24-ceres

以下是使用Ceres求解器实现BA的示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
// 定义相机参数结构
struct CameraParameters {
    double f;      // 焦距
    double k1, k2; // 径向畸变参数
    double tx, ty, tz; // 平移向量
    double rx, ry, rz; // 旋转向量（轴角表示）
};

// 定义观测数据结构
struct Observation {
    int camera_id;
    int point_id;
    double x, y;  // 观测到的像素坐标
};

// 重投影误差结构
struct SnavelyReprojectionError {
    SnavelyReprojectionError(double observed_x, double observed_y)
        : observed_x(observed_x), observed_y(observed_y) {}

    template <typename T>
    bool operator()(const T* const camera,
                   const T* const point,
                   T* residuals) const {
        // 相机参数: [f, k1, k2, tx, ty, tz, rx, ry, rz]
        T p[3];
        // 将点从世界坐标系转换到相机坐标系
        ceres::AngleAxisRotatePoint(camera + 6, point, p);
        p[0] += camera[3];  // tx
        p[1] += camera[4];  // ty
        p[2] += camera[5];  // tz

        // 投影到图像平面
        T xp = p[0] / p[2];
        T yp = p[1] / p[2];

        // 应用径向畸变
        T r2 = xp*xp + yp*yp;
        T distortion = 1.0 + camera[1] * r2 + camera[2] * r2 * r2;

        // 计算最终投影点
        T predicted_x = camera[0] * distortion * xp;
        T predicted_y = camera[0] * distortion * yp;

        // 计算残差
        residuals[0] = predicted_x - T(observed_x);
        residuals[1] = predicted_y - T(observed_y);

        return true;
    }

    static ceres::CostFunction* Create(const double observed_x,
                                     const double observed_y) {
        return (new ceres::AutoDiffCostFunction<SnavelyReprojectionError, 2, 9, 3>(
            new SnavelyReprojectionError(observed_x, observed_y)));
    }

    double observed_x;
    double observed_y;
};

// 主函数
void BundleAdjustment(const std::vector<CameraParameters>& cameras,
                     const std::vector<Eigen::Vector3d>& points,
                     const std::vector<Observation>& observations) {
    // 创建优化问题
    ceres::Problem problem;

    // 为每个观测添加残差块
    for (const auto& obs : observations) {
        const auto& camera = cameras[obs.camera_id];
        const auto& point = points[obs.point_id];

        // 构建相机参数数组
        double camera_params[9] = {
            camera.f, camera.k1, camera.k2,
            camera.tx, camera.ty, camera.tz,
            camera.rx, camera.ry, camera.rz
        };

        // 构建点参数数组
        double point_params[3] = {
            point.x(), point.y(), point.z()
        };

        // 添加残差块
        ceres::CostFunction* cost_function =
            SnavelyReprojectionError::Create(obs.x, obs.y);
        
        problem.AddResidualBlock(cost_function,
                               nullptr,  // 不使用鲁棒核函数
                               camera_params,
                               point_params);
    }

    // 配置求解器
    ceres::Solver::Options options;
    options.linear_solver_type = ceres::SPARSE_SCHUR; // 稀疏舒尔补
    options.minimizer_progress_to_stdout = true;
    options.max_num_iterations = 100;
    options.num_threads = 4;

    // 求解
    ceres::Solver::Summary summary;
    ceres::Solve(options, &problem, &summary);

    // 输出结果
    std::cout << summary.FullReport() << "\n";
}

// 使用示例
int main() {
    // 创建测试数据
    std::vector<CameraParameters> cameras;
    std::vector<Eigen::Vector3d> points;
    std::vector<Observation> observations;

    // 添加相机
    cameras.push_back({1000.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0});

    // 添加三维点
    points.push_back(Eigen::Vector3d(1.0, 2.0, 3.0));

    // 添加观测
    observations.push_back({0, 0, 100.0, 200.0});

    // 执行BA优化
    BundleAdjustment(cameras, points, observations);

    return 0;
}

代码说明：

1. 数据结构：
   • CameraParameters：存储相机内参和外参
   • Observation：存储观测数据
   • SnavelyReprojectionError：计算重投影误差
2. 优化过程：
   • 使用Ceres求解器
   • 配置为使用舒尔补求解器
   • 支持多线程优化
3. 主要特点：
   • 使用自动微分计算雅可比矩阵
   • 支持相机畸变模型
   • 可以处理大规模BA问题
4. 使用建议：
   • 根据实际需求调整相机参数模型
   • 可以添加鲁棒核函数处理外点
   • 根据问题规模调整求解器参数

使用Ceres求解BA问题具有以下优势：

1. 自动微分：
   • 无需手动推导和实现雅可比矩阵
   • 减少代码错误，提高开发效率
   • 支持复杂的非线性函数
2. 求解器选择：
   • 提供多种线性求解器（DENSE_QR, SPARSE_NORMAL_CHOLESKY等）
   • 特别优化了SPARSE_SCHUR求解器，适合大规模BA问题
   • 可以根据问题规模自动选择最优求解器
3. 并行计算：
   • 支持多线程优化
   • 可以充分利用多核CPU
   • 提供线程安全的实现
4. 鲁棒性：
   • 内置多种鲁棒核函数（Huber, Cauchy等）
   • 可以有效处理外点
   • 提供参数边界约束
5. 灵活性：
   • 支持自定义损失函数
   • 可以方便地添加新的参数块
   • 支持多种参数化方式（四元数、李代数等）
6. 性能优化：
   • 使用稀疏矩阵存储
   • 实现了高效的舒尔补计算
   • 支持问题规模的动态调整
7. 调试功能：
   • 提供详细的优化过程信息
   • 支持问题诊断和性能分析
   • 可以输出中间结果

3.2 其他优化库

除了Ceres，还有其他优秀的优化库可以用于BA问题：

1. g2o (General Graph Optimization)：
   • 基于图优化的通用框架
   • 优点：
     • 提供完整的图优化接口
     • 支持多种优化算法
     • 适合SLAM等图优化问题
   • 缺点：
     • 配置相对复杂
     • 需要手动实现雅可比矩阵
     • 文档相对较少
2. Ceres vs g2o：
   • 实现难度：
     • Ceres：自动微分，实现简单
     • g2o：需要手动推导雅可比矩阵
   • 性能：
     • Ceres：大规模问题性能更好
     • g2o：小规模问题可能更快
   • 灵活性：
     • Ceres：更适合通用优化问题
     • g2o：更适合图优化问题
3. 其他选择：
   • Eigen：提供基础矩阵运算，可以自己实现优化
   • GTSAM：基于因子图的优化库，适合SLAM
   • NLopt：提供多种非线性优化算法
   • Ipopt：适合大规模非线性优化问题
4. 选择建议：
   • 如果是BA问题，推荐使用Ceres
   • 如果是图优化问题，可以考虑g2o或GTSAM
   • 如果需要更多控制，可以考虑自己实现

4. Related Works

还有各种进阶BA算法：

• Parallel BA
  • Ni et al. 2007, Wu et al. 2011 (PBA)
• Hierarchical BA
  • Steedly et al. 2003, Snavely et al. 2008, Frahm et al. 2010
• Segment-based BA
  • Zhu et al. 2014, Zhang et al. 2016 (ENFT)
• Incremental BA
  • Kaess et al. 2008 (iSAM), Kaess et al. 2011 (iSAM2), Indelman et al. 2012 (iLBA), Ila et al. 2017 (SLAM++), Liu et al. 2017 (EIBA), Liu et al. 2018 (ICE-BA)

4.1 Parallel BA

并行BA主要利用问题的稀疏性和可分解性，将优化问题分配到多个计算单元上。主要方法包括：

1. 数据并行：将观测数据分配到不同处理器
2. 模型并行：将相机和点参数分配到不同处理器
3. 混合并行：结合数据并行和模型并行的优点

4.2 Hierarchical BA

层次化BA通过构建多分辨率的问题表示来加速优化：

1. 粗到细策略：先在低分辨率上优化，再逐步细化
2. 多尺度表示：使用图像金字塔或特征金字塔
3. 自适应优化：根据问题规模动态调整优化策略

4.3 Segment-based BA

基于分段的BA将问题分解为多个子问题：

1. 空间分段：根据空间位置将场景分成多个子区域
2. 时间分段：根据时间序列将问题分成多个子问题
3. 混合分段：结合空间和时间信息进行分段

4.4 Incremental BA

增量式BA主要用于在线SLAM系统：

1. 滑动窗口：维护固定大小的优化窗口
2. 边缘化：将旧状态边缘化以保持计算效率
3. 稀疏更新：只更新受新观测影响的部分

Contact

Feel free to contact me windmillyucong@163.com anytime for anything.

License

Creative Commons BY-SA 4.0

• Previous
  优化理论基础
• Next
  凸优化